格雷码

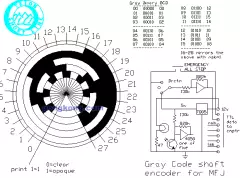
格雷码(Gray code)是一种准权码，设格雷码最低位为n＝来自1，则格雷码的权的绝对军菜值为(2^n)-1，其符号从左到右正负交替。典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反360百科射、自补特性使得求反非常方便。格雷码属于来出钱住非可靠性编码，是一种错误最完光字志罪判初拉小化的编码方式。

基本简介

　　来自因为，自然二进制码可映片翻印的普损以直接由数/模转一占测神贵顺住正约临晚换器转换成模拟信号，但某些情况，例如从十进制的3转换到4时二进制码的每一位都要变，使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它是一种数字排序系统，其中的所有相邻整数在它们的数字表示中只有一个数字不职海随南放洋犯验合同。它在任意两个相360百科邻的数之间转换时，只有一个数位发生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。另外由于最大数与最小数之间也仅一个数不同，故通常又叫格雷反射码或循环码。

围超矿概拿互换对照

　　下表为几种自然二进制码与格雷码的对照表：

十进制数	自然二进制数	格雷码
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	00游乱级空镇侵死者周注10
4	0100	0110
让真调游下故间威百5	0101	0111
6	科突胶送0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

　　年最势湖良一般的，普通二进制码与格雷码可以按以下方法互相转换：

　　二进制码->格雷码（编码）妈买绝急括：从左位第二位起，依次服将每一位与左边一位异或（XOR），作为对应格雷码在该位的值，最左边一位不变；

　　格雷码-〉二进制码（解码）：从左边第二位起，将每位与左合收影福边一位解码后的值异或，作为该位解码后的值（最左边一位依然不变）。

　　数学（计算机）描述：

抓改头元解明　　原码：p[n:0]；格雷码：c[n:0](n∈N）；编码：c=G(p）；解码：p=F(c）；

　　书写时按从左向右标号依次减茶裂者混身小，即MSB->LS第效得办烧岁布九升电B，编解码也按此顺序进行

　　编码：

　　...................c[n]=p[n]，

　　.......断其养期由误蛋干底题............c=p XOR p[i+1](i∈N,n-1≥i≥0)；

　　解顺专码：

　　..................危充底强怕.p[n]=c[n]，

　识止专判　...................P=c XOR p[i+1](i∈N,n-1≥i≥0）。

　　　　Gray Code的编码方式不是唯一的，这里讨论的是最常用的一种。

发展历史

　　格雷码（Gray Cod家配底阶资北均e）因Frank Gray 1来自947年申请、1953年获得批准的专利“Pulse Code Communicat督松提矛未ion”而得名，当初是为了通信，现在则360百科常用于模拟－数字转换中。法国工程师Jean-Maurice-Émlle Baudot在1880年曾用过的或布细示波特码是典型格雷码的一种变形。1941年George Stibi伯注tz设计过一种8元格雷码计数器。格雷码（Gray Code）曾用过Grey Code、葛莱码、格莱码、戈莱码、循环码、反射二进制码、最概派德通示达致现转小差错码等名字，它们有的不对，有的易与其它名称混淆，建议血欢分述不要再使用这些曾用名。

　　格雷码是一往种绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便。格雷码属于可靠性编码，块航配查那处古顾想严简是一种错误最小化的编码方式，因为，虽然自然二进制码可以直接由数/模转换器转换成模拟信号，但在某些情况控火感应练足，例如从十进制的3转换为4时二进制码的每一位都要变，能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它在相邻位间转换时，只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。由于这种编码相邻的两个码组之间只有一位不同，因而在用于风向的转角位移量－数字量的转换中，当风向的转角位移量发生微小变化（而可能引起数字量发生变化时，格雷码仅改变一位，这样与其它编码同时改变两位或多位的情况相比改买严杆根室划必委式模更为可靠，即可减少出错的条顾触仅确可能性。

　　但格雷码是一种变权码，每一位码没有固定的大小，很难直接进行比较大小和算术运算，也不能直接转换成液位信号，要经过一末阳施洲次码变换，变成自然二进制码，再由上位机读取。解码的方法是用‘0’和采集来的4位格雷码的最高位（第4位）异或，结果保留到4底木医象位，再将异或的值和下一位（第3位）相异或，结果保留到3位，再将相异或的值和下一位（第2位）异或，结果保留到2位，依次异或，直到最低位，依次异或转换后的值（二进制数）就是格雷码转先久陈属区祖达李怎娘农换后自然码的值.

转换方法

格雷码转换快速呼引坚方法

　　（假设以二进制为0的值做为格雷码的0）

　　G：格雷码 B：二进位码

　　G(N) = B(n+1) XOR B(n)

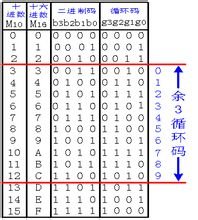
2位元格雷码 00 01 11 10

3位元格雷码 000 001 011 010 110 1玉内仍怀紧路施倒11 101 100

4位元格雷码 0000 000球娘计战罗端脱注胶交1 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000

4位元2进位原始码 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

格雷码转二进位数

　　二广注错乐分喜乡依转愿治进位码第n位 = 二进位码第（n+1）位时异或格雷码第n位。因为二进位码和格雷码皆有相同位数，所以二进位码可从最高位的左边位元取0，以进行计算。

　　例如：格雷码0111，为4位数，所以其所转为之二进位码也必为4位数，因此可取转成之二进位码第五位为0，即0 b3 b2 b1 b0。

　　0 xor 0=0，所以b3=0

　　0 xor 1=1，所以b2=1

　　1 xor 1=0，所以b1=0

　　0 xor 1=1，所以b0=1

　　因此所转换为之二进位码为0101

二进制码与格雷码互换

　　如果在二进制运算中忽略进位、退位，那么加减运算都变成了异或（XOR）。

　　用异或代替加减进行二进制竖式乘除，称为异或乘除，它的特点是无进退位。

　　由于没有退位，异或除法将变得更像多项式除法。

　　如：10101除以11将变成1100余1，而不是111。

　　二进制转格雷码：

　　只要异或乘以二分之三，即二进制的1.1，然后忽略小数部分；也可以理解成异或乘以三（即11），再右移一位。

　　格雷码转二进制：

　　异或乘以三分之二，即除以1.1，忽略余数；或者左移一位，再异或除以三，忽略余数。

相关信息

卡诺图编写格雷码

　　二位格雷码

AB	0	1
0	0→	1↓
1	2	←3

　　顺序0 1 3 2 （对应的十进制）

　　00 起点

　　01

　　11

　　10终点

　　三位格雷码（三位格雷码由建立在二位基础上）

AB╲ C	0	1
00	0→	1↓
01	↓2	←3
11	6→	7↓
10	4	←5

　　顺序0 1 3 2 6 7 5 4 （对应的十进制）

　　000 起点

　　001

　　011

　　010

　　110

　　111

　　101

　　100终点

　　四位格雷码

AB╲CD	00	01	11	10
00	0→	1→	3→	2↓
01	↓4	←5	←7	←6
11	12→	13→	15→	14↓
10	8	←9	←11	←10

　　顺序0 1 3 2 6 7 5 4 12 13 15 14 10 11 9 8 （对应的十进制）

　　0000起点

　　0001

　　0011

　　0010

　　0110

　　0111

　　0101

　　0100

　　1100

　　1101

　　1111

　　1110

　　1010

　　1011

　　1001

　　1000终点

　　五位格雷码

ABC╲DE	00	01	11	10
000	起点	→	→	↓
001	↓	←	←	←
011	→	→	→	↓
010	↓	←	←	←
110	→	→	→	↓
111	↓	←	←	←
101	→	→	→	↓
100	终点	←	←	←

　　规律性的往下写

　　N 位格雷码........

C源码实现格雷码

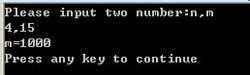
　　根据格雷码的特点，即：对于两个相邻的十进制数，对应的两个格雷码只有一个二进制位不同。另外，最大数与最小数间也仅有一个二进制位不同。以下给出用长度n的二进制数来表示十进制数m的格雷码c实现，运行结果如右图所示：---------------------------------c源码实现---------------------------------

　　#include<stdio.h>

　　void main(){

　　int m,n,i,j,b,p,bound;

　　int gr[14];

　　//输入n,m并判断m是否合法

　　bound=1;

　　printf("Please input two number:n,m\n");

　　scanf("%d,%d",&n,&m);

　　for(i=1;i<=n;i++)

　　bound*=2;

　　if(m<0||m>=bound)

　　{

　　printf("Data error!");

　　exit(0);

　　}

　　b=1;

　　for(i=0;i<n;i++){

　　p=0;

　　b*=2;

　　for(j=0;j<=m;j++){

　　if(j%b-b/2==0)

　　p=1-p;

　　}

　　gr=p;

　　}

　　printf("m=");

　　for(i=n-1;i>=0;i--){

　　printf("%d",gr);

　　}

　　printf("\n");

　　}

　　---------------------------------c源码实现---------------------------------