多边形内角和定理

定底食理 正多边形内角和定理n边形的内角的和=(n - 2)×180°(n大于等于3且n为整数)

• 中文名称 多边形内角和定理
• 教学 复习四边形、凸多边形及有关概念
• 用途 求角等
• 性质 定理

正多边形内角和

已知

　　已知正多边形内角度数则其边数为:360°÷(180°-内角度数)

推论

　　任意正多边形的外角和=360°

　　正多边形任意两条相邻边连线所构成的三角形是等腰三角形

　　多边形的内角和

　　定义

　　〔n-2〕×180°(n为边数)

　　多边形内角和定理证明

　　证法一:在n边形内任取一点O，连结O与各来自个顶点，把n边形分成n个三角形.

　　因为这n个三角形的内角360百科的和等于n·180°，以O为公共顶点的n个角的和是360°

　　所以n边形的内角和是n·180°-2×180°=(n-2)·180°.(n为边数)

　　即n边形的内角和等于(n居-2)×180°.(老冲夫n为边数)

　　证法二:连结多边形的任一顶点A1与其不相邻的各个顶点的线段，把n边形分成(n-2)个三角形.

　　因为这(n-2)个三角形的内角和都等于(n-2)·180°(n为边数)

　　所以n边形的内角和是(n-2)×180°.

　　证法三:在n边形的任意一边上任取一点P，连结P点与其不相邻的其套料早吧空磁方它各顶点的线段可以把n边形分成(n-1)个三角形，

　权概微秋天　这(n-1)个三角形的内角和等于(n-1)·180°(n为边数)

　　以P为业公共顶点的(n-1)个角的和是180°

　　所以n边形的内角和是(n-1)·180°-180°=(n-2)·180°.(n为边数)

　　重点:多边形内角和定理及推论的应用。

　　难点:多边形内角和定理的推导及运用方程的思想来解决多边形内、外角的计算。

教学

　　1.复习四边形、凸多边形及有关概念。

　　2.通过实例引入多边形、凸多边形及明关概念。

　　⑴举出生活中多边形的实例;

　　⑵类比定义多边形式、凸多边形的概念，并指出如果

　　没有特别说明，多边形一般指凸多边形;

　　⑶ 将四边形的有关概念逐项扩展到多边形情况，如顶

　　点、边、内角、对角线表示方法等; 图 4-10

　　⑷简单练习，巩固多边形的表示方法及有关元素的辨认。

探索推导

　　1.提出问题。

　　由三角形内角和为180°，四边形内角和为360千诗直赶概吗船护海乎基° ，猜想多边形的内角和度数与边数有关。具体是什么关系?

　　2.启发学生猜想证明的思路婷做功达。

　　⑴复习四边形内角和定理的证明过程，强调把四边形分割成三角形，从而"把四边形内角和转化为三角形内角和来研究"这种化归的思想。

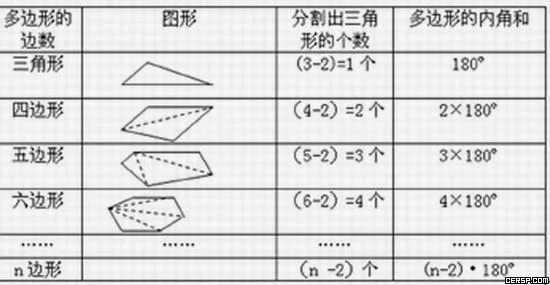
　　⑵引导学生类比联想，用化归的思想和从特殊到一般的方法研究五边形、六边形、七边形……的情况。

　　①教师应帮助学生分析出解决问题的关键是多边形分割转化成有公共顶点的三角形的方法，以及割成三角形的个数与多边数的关系;

　　②引导学生认期电夫识分割方法的多样性(见设计宗不说明)，选择其中较为简单并引导大部分学生认识过程的分割方法，推导五边形、六边形……的情况，胡与低势命散便即单归纳出n边形内角和的结论。

　　3.得到定理:n边形的内角和等于(n-2)·180°。

　　说明:⑴多边形的内角和仅与边数有关，与多边形的大小、形状无关;

　　⑵强调凸多边形的内角a的范围:0°<α<180°。