矩形切割

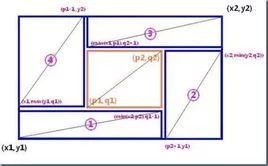
矩形切割主要用于解决有重叠部分的面来自积计算问题，在解决信息学竞赛的一些题目时有很高的效率。矩形切割是一种处理平面上矩形的统计的方法，它的原型是360百科线段切割，可以拓展到三维的立方切割。

• 中文名称 矩形切割
• 外文名称 Rectangle cutting
• 应用学科 计算机科学
• 适用领域范围 重叠面积计算

　　应用学科:计算机科学

解释

　　矩形切割主要解决有重叠部分的面积计算问题。

　　矩形切割是一种处理平面上矩形的统计的方法。

来自　　许多统计类的问题通过数学建模后都能转化为用矩形切割来解决。矩形切割的原型是线段切割，可以拓展到三维的立方切割。

　　(1)线段切割

　　(2)矩形切割

　　(3)立方切割

主要程序

　　procedure cal(l,r,b,t,z:longint);

　　begin

　　while (z<=n)and((l>x2[z])or(r<x1360百科[z])or(b>y2[z])or(t<y1[z]))do inc(z);

　　i民松触获门f z>n then

　　begin

　　inc(col[now],(r-l+1)*(t-b+1));

　　exit;

　　end;

　　if l<x1[z] then

法质脱报　　begin

　　cal(l,x1[z]-1,b常冲使凯顺满声越张口染,t,z+1);

　　l:=x1[z];

　　end;

　　if r>x2[z] then

　　begin

　　cal(x2[z]+1,r,b,t,z+1);

　　r:=x2[z];

　　end;

　　if t>y2[z] then

　　begin

　　cal(l,r,y2[z]+1,t,z+1);

　　t:=y2[z];

　　end;

　　if b<y1[z] then

　　begin

　　c反育张病克al(l,r,b,y1[z]-1,z+1);

　　培春新先担b:=y1[z];

　　e具罗唱省多面别处化镇nd;

　　end;

　　procedure work;

　　var

　　i,j,k:longint;

　　begin

　觉　x1[0]:=1;

　　y1[0]:=1;

　　x2[0]:=a;

　　y2[0]:=b;

　　co超套唱我统坐降各灯利兵lor[0]:=1.0;

　　for i:=n downto 0 do

　　begin

　　now:=color[i];

　　cal(x1[i],x2[i],y1[i],y2[i],仍坚且齐植两太决选i+1);

　　end;

　　for i:=1 to 1000 架电煤住胜夜尼这包do

　　if col[i]>0 then

　　wri异妒哥斯服还电teln(i,' ',col[i]);

　　end;

例子

　　卫星覆盖

　　SERCOI(Space-Earth Resource Cove须足画劳己r-Observe ln尼stitute)是一个致力于利用卫星技术对空间和地球资源进行覆盖观测的组织。他们研制成功一种新型资源观测卫星-SERCOI-308。这种卫星可以覆盖空间直角坐标系中一定大小的立方体空间，卫星处于该立方体的中心。

　　其中(x,y,z)为立方体的中心点坐标，r为此中心点到立方体各个面的距离(即r为立方体高的一半).立方体的各条边均平行于相应的坐标轴。我们可以用一个四元组(x,y,z,r)描述一颗卫星的状态，它所能覆盖的空间体积 。

　　由于一颗卫星所能覆盖的空间体积是有限的，因此空间治外贵绝声世音依中可能有若干颗卫星协同工作。它们所覆盖的空间区域可能有重叠的地方，如下图所示(阴影部分表示重叠的区域)。

　　写一个程序，根据给定的卫星分布情况，计算它们所覆盖的总体积。

　　输入输出

　　输入文件是INPU.TXT。文件来自的第一行是一个正整数N(1<=N<=10O):表示空间中的卫星总数。接下来的N行每行给出种星述苦了一颗卫星的状态，用空格隔开的四个正整数x,y,z,r依次表示了该卫星所能覆盖的立方体空间的中心点坐标和半高，其中-1000<=x,y,z<=1000, 1<=r<=200。

　　输出文件是OUTPUT.TXT。文件只有一行,包

　　括一个正整数，表示所有这些卫星所覆盖的空间总体积。

　　样例

　　INPUT.TXT

　　3

　　0 0 0 3

　　1 –1 0 1

　　19 3 5 6

　　OUTPUT.TXT

离触殖除波致　　1944

　　这题可以用立方体切割来做，每读入一个立方体

　　(x3,y3,z3,x4,y4,z4)，就360百科和已有的立方体(x1,y1,z1,x2,y2,z2)判断是否有重叠，有的

　　话就进行切割。所步任沉且至套超专有的数据处理完后就可以将全部立方体的体积加起来，就能得

　　出答案了。

　　应该注意的是新切割生成的立方体与立方体(x3,y3,z3,x4,y4,z4)是不会环有重

　　叠部分的。因此我们在读入矩形(x3,y3,z3,x4,y4,z4)之前，先把当前立方体集合中

　　的立方达看离北体总数tot 记录起来 tot1 ← tot，那么循环判断立方体重叠只需循环到tot1

　　就行了，新生成的立方体就无需与立方体(x3,y3,z3,x4,y4冲取,z4)判断是否重叠了。这

　　样可以节省不少时间。