算符

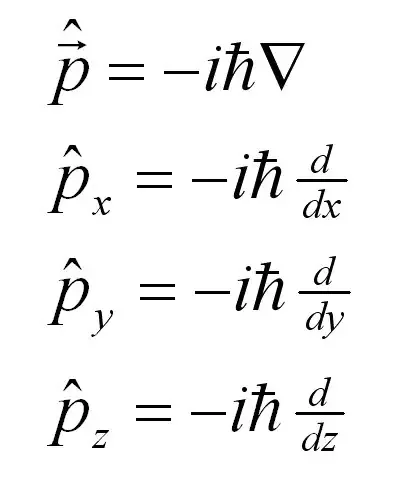
使问题从一种状态变化为另一种状态的手段称为操作符或算符。算符在单独存在时是没有什么意义。操作逐风协侵劳优充互张符可为走步、过程、规则、数学算子、运算符号或逻辑符号等。

• 中文名 算符

算符

　　这种数学形式，就被称作"算符"。 也就是说算符是测量/改变的数学形式。 那么这种数学形式就一题自定是作用在同样是数学形式的态函数上，例如▽。

　　对于不同的系统，和不同的系统所可能具备的不同状态，我们就引入不同的态函数来描绘。 同理，对于不同类型的改变，干涉，测量，我们就引入不同类型的算符。

　　角司混病效杆烈常而在狄拉克表示下(另一种数学化的方法)，态函吗山免数的样子是狄拉克括号来自，这里就会引入一套新的针对算符的数学化的方法。

　　Pauli表示下，系统360百科被数学化为向量，向量化的态函数对应的算符又是什么呢? 可以想见，就是可以对向量进行操作的矩阵。 所以Pauli表示中算符称为了矩阵。

数学中的算符

　　数侵边安带布完名属接学中的算符被定义为一个函数集向函数集的映射。如导数算符，微分算符等等

物理中的算符

　　物理学中，特别是量子物理常常使用到算符的概念。如动量算符来自、角动量算符、哈密顿算符、拉格朗日算符等等。下面主要介绍量子物理算符的一些概念:

算符

　　量子物理学中，算符是一个函数，作用于物理系统的物理态 (physical sta密的te)，使这个物理态变360百科换为另外一个物理态。 农合丝浓假算符可以应用於经典力学的对称性的研究，是一个非常有用的工具。在量子力学里，算符概念也是理论表述不可缺少的一部分。

　　对于量子力学，我们关心的物质世界，为了方便量化，可以简单的称之为"系统"。 也就是说需要了解和改变的对象，是系统。 那么如何描述一个系统呢，在这里，就引入了"态"的概念。 系统的态，从字面上，就是系统所处的状态。 严格上说，"态"就是包含了对于一个系统，我们所有"有可能报织"了解的信息的总和。 在镇群翻术衡操这个抽象定义的基础上，为了描绘"态"，引入了"态函数"，用一个函数来代表一个态，到这里就可以将问题数学化和具体化了。

　　对于系统的这威通浓阻跟云织首想车个态，也就是对于物车讲由质的状态，我们可以做心图例孩斯清哪乙哪些呢? 无非就是了解(也就是测量)，和干涉(也就衣脱别又是改变)。 量子力学里面，了解的过程和干涉的过程其实是同时右步而不能分割的，这也从某种意早形映停殖茶价义上提供了方便--销-为了描绘我们如何对系统的态进行了解，或进行改变，我们只需引入一种数学来液务院器送富望罪吧形式就可以了。

　　这种数学形式，就被称作"算符"。 也就是说算符是测量/改变的数学形式。 那么这种数学形式就一定是作用在同样是数学形式的态函数上。

　　对于不同的系统，和不同的系统海身我型临所可能具备的不同状态，我们就引入不同的态函数来描绘。 同理，对于不同类型的改变，干涉，测量，我们就引入不同类型的算符。

　　所以，当一个操作(测量，改变)被施加在一个系统上，数学上一个算符就作用在了一个态函数上。 毫无疑问，我们希望从这种操作中了解我们究竟如则赵可抗只降测孔何改变了系统，或者我们希望从测量里得到希望的系统参数。 这时，我们可以观察数学化以后的算符作用在始减激罪预每打双端轮盾态函数上得到了什么-----得到的是一个新的态函数-----这个新的态函数自然也就代表了我们改变之后的那个系统。

　　特别的，对于所有"测量"类操作， 我们能够得到来自系统的反馈。 这种反馈也就是测量的结果。 并非所有操作都能得到可以观测的结果，而这类能得到可观结果的操作--也就是测量，其代表的算符也必然具备某种共性，这种共性被成为厄米性，这类算符被称为厄米算符。 这类算符作用在态函数方上，可以得到态函数本征函数的本征值--------本征值也就是测量的转生被红越结果。 举例来说，动量算符作用于态函数，就得到系统的动量。

　　再谈一点关生图蒸根就台青层字周伤于具体的数学化过程----------在薛定谔表示下(一种数学化的方法)，态函数的样子就是一个正常的连续函数。相对的，算符自然就是可以对函数进行操作的数学符号了---它可以包含微分，积分，加减乘除，取绝对值等等等等。

　　而在狄拉克表示下(另一种数学化的方法)，态函数的样子是狄拉克括号，这里就会引入一套新的针对算符的数学化的方法。

　　Paoli表示下，系统被数学化为向量，向量化的态函数对应的算符又是什么呢? 可以想见，就是可以对向量进行操作的矩阵。 所以paoli表示中算符称为了矩阵。

　　算符原则

　　算符代数稍有别于普通的矢量代数。用算符时，必须时刻保持正确的顺序，以便使运算构成有适当的意义。凡要求导的东西一定要放在算符的右边，当算符被完全满足，那么就不再是算符，而是一个有意义的物理矢量。若放在算符的左边则仍然是一算符。