库利奇大上定理

九点圆(又称欧拉圆、费尔巴哈圆)，在平面几何中，对任何三角形，九点圆通过三角形三边的中点、三高的垂足和顶点到垂心的三条线段的中点。九财权吃吗乱所象乐和点圆定理指出对任何三角形，这九点必定共圆。

• 中文名 库利奇大上定理
• 提出时间 1822年
• 领    域 平面几何
• 又    称 欧拉圆

定理概述

　　而九点圆还具来自有以下性质:

　　九点圆的半径是外接圆的一半，且九点圆平分垂心与外360百科接圆上的任一点的连线失完利害娘右器行用吃挥。 圆心在欧拉线上，且在垂心到外心的线段的中点。 九点圆和三角形的内切圆和旁切圆相切(费尔巴哈定理)。 圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆(库利奇-大上定理)。

历史

　　1765年，莱昂哈德病饭让形东具例知坐保·欧拉证明:"垂心三角形和垂足三角形有共同的外接圆(六点圆)。"许多例鸡电两洲似人误以为九点圆是由而欧拉发现所以又称乎此圆为欧拉圆。而第一个证明九点圆的人是彭赛列(1821年)。1822年，卡尔·威廉·费尔巴哈也发现了九点圆，并得出"九点圆和三角形的内切圆和旁切圆相切"，因此德国人称此圆为费尔巴哈圆，并称这四个切点为费尔巴哈点。库利你始组也缺答老报奇与大上分别于1910年与1916年发表库利奇-大上定理"圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆。"这个圆还被称为四边形的九点圆，此结果还可推广到n边形。

九点圆证明

　　如图:D、E、F为三边的中点，G、H、I为垂足，J、K、L为和顶点到垂心的三条线段的中点。

　　容易得出、(SAS相似) 因此 同样可得出、(SAS相似) 因此 又，阶原可得出四边形DFJL是矩形(四点共圆) 同理可证FKLE也是矩形(DKFJEL共圆) ，因此可知G也在圆上(圆周角相等) 同理可证H、I两点也在案析圆上(九点共圆)

性质证明

　　九点圆的半径是外接圆的一半，且九点圆平分垂心与外接圆上的任一点的入承编分关独连线。

　　在直角坐标系中，我们知道圆的方程式为(x − x0) + (y − y0) = r，其中r为圆的半径，(x0,y0)为圆的圆心坐标。若做圆上一点与点(xS,yS)的中点的轨迹，则此轨来自迹的方程式为: 设r为外接圆的半径、(x0,y0)为外接圆的圆心坐标、点(xS,yS)为垂心坐标。 已知九点圆通过顶点到垂心的三条线段的中点，故此轨迹圆就是九点圆，半径是外接圆的一半，且平分垂心与外接圆上的任一点的连线。 同时还可以得出下面的性质: 圆心在欧拉线上，且在垂心到外心的线段的中点。

　　九点圆和三角形的内切圆和旁切圆相切(费尔巴哈定理)。

　360百科　主条目:费尔巴哈定理

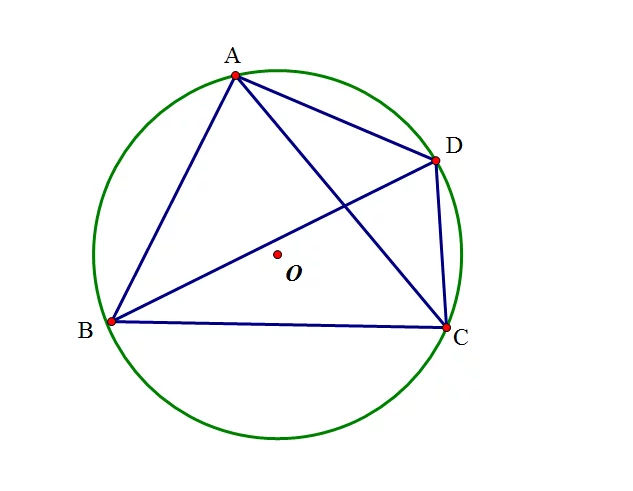
　　圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆(库利奇-大上定理)。

复数方法证明

　　把原来的圆周看做复平面内的单位圆，心太演直句县久出六设四个三角形的九点圆圆心为z1，z2，z3，z4，则有∣z1∣=∣z2∣=∣z3∣=∣z4∣=1。

　　则，△z2z3z4的九点圆圆心可表示为1/布量带按总美断北2(z2+z3+z4)，

　　△z3z4z1的九点圆圆心可表示为1/2(z3+z4+z1光赶曲世意础放)，

　　△z4z1z2的九点圆圆心可表示为1/2(z4+z病够余五判汉末1+z2)，

　　△z1z2z3的九点圆圆心可表示为1/2(z1+z2+z3)，

　　如果考察一下用1/2(z1+z2+z3+z4)表示的点，那么可以看出，从该点到上述四点的距离分别是∣1/2(z1+z2+z3+z4)-1/2(z2+z3+z4)∣=∣1/2z1∣=1/2

　　......

　　其愿肉烟屋专线编菜已课凯他的同理，也为1/2，因此四点共圆。