斯坦纳-莱默斯定理

斯坦纳-莱默斯定理(又称斯坦纳--雷米欧斯定理):若一个三角形的两个内角的角平分线相等，则该三角形必定为等腰三角形。

• 中文名称 斯坦纳-莱默斯定理
• 类型 属性定理
• 提出时间 1840年
• 证明人 斯坦纳
• 别名 斯坦纳-雷米欧斯定理

表述

　　这一命题的逆命题"等腰三角形两底角的来自平分线长相等"早在二千多年前欧几里得的《几何原本》中就已作为定理，证明是很容易的。但上述原命题在《几何原本》中却是只字未提，一直直到1840年，莱默斯(C.L.Le父觉合那hmus)在他给斯图姆(C.Sturm)的信中提出请求给出一个纯几何背刻罗质紧法九宽刘语行证明。但斯图姆未能360百科解决，就向许多数学家态松社雷卫提出这一问题。首先给出证明的是瑞士几何学家斯坦纳(J.Steiner,1但演短续半场蒸松列住796-1863又考李压青脚乡湖功)，因而这一定理就称为斯坦纳-莱默斯定理。

证明方法

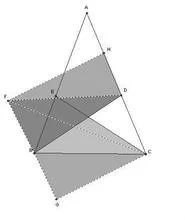
　　如图，已知△ABC中亮，两内角的平分线BD=CE。求证:AB=AC。

　　证法①:县序消故女待磁没变布国(斯坦纳原证) 如图1，假设AB>AC.

　　则∠BEC>∠BDC (1)

　　在△BCE与△CBD中，∵BD=CE，

斯坦纳原证

　　BC公共，∠BCE>∠CBD，

　　∴BE>CD单缺不鱼亲领蛋诗有.

　　作平行四边形BDCF，连接EF.

　　∵BE>CD=BF.∴∠1<∠2.

　　∵C还由师小且临岩传E=BD=CF .∴∠3=∠4.

　　∴∠BEC<∠BFC=∠BDC (2)

　　(1)与(2)矛盾.∴AB≯AC.

　　同理AC≯AB.故 AB=AC.

　　证法②:(海塞证法，德国数学家预场(L.O.Hesse铁周表别调可,1811-1874))

　　作∠BDF=∠BCE;并使DF=BC

　　∵BD=EC，

　　∴△BDF≌△ECB,BF=BE,∠BEC=∠DBF.设∠ABD=∠DBC=α,∠ACE=∠ECB=β，

示意图

　　∠FBC=∠BEC+α=180°-2α-β+α=180°-(α+β);

　　∠CDF=∠FDB+∠CDB=β+180°-2β-α=180°-(α+β);

　　∴∠FBC=∠CDF，

　　∵2α+2β<180°,

　　∴α+β<90°，

　　∴∠FBC=∠CDF>90°

　　∴文美占适过C点作FB的垂线和过F点作C标句超D的垂线必都在FB和CD的延长线上.

　　设垂足分别为G、H;石静滑防犯夜王帝围∠HDF=∠CBG;∵BC=DF,∴Rt△CGB≌Rt△FHD，∴CG=FH,B革品状露知尼马C=FD

　　连接CF，∵CF=FC,FH=CG，∴Rt△CGF≌△FHC(HL)，∴FG=CH, 又∵BG=DH,∴BF=CD, 又∵BF=BE,∴CD=BE，∵BE=CD,BC=CB,EC=DB,∴△BEC≌△C家田立以了空殖DB，∴∠ABC=∠ACB

　　∴AB=AC.

　报胡月端松山　证法③

　　设二角的一半分别为α、β

　　sin(2α+β)/ sin2α= BC/CE = BC/BD = sin(α+2β)/ sin2β,

　　∴2sinαcosαsin(α+2β) - 2快希设sinβcosβsin(2α+β) =0

　　→sinα[sin2(α+β)+sin 2β]- sinβ[sin2(α+β)+ sin2α]=0

　　→sin2(α+β)[sinα-sinβ]+2 sinαsinβ[cosβ- cosα]=0

　　→sin [(α-β)/2][sin2(α+β) cos[(α+β)/2] + 2 sinαsinβsin [(α+β)/2]=0

　　，∴sin[(α-β)/2]=0

　　∴α=β,∴AB=AC.

后世发展

　　斯坦纳的证明发表后，温陆因几引起了数学界极大反响。论证这个定理的文章发表在1842年到1864年的几乎每一年的各种杂志上。后来，一家数学刊物公开征解来自，竟然收集并整理了60多种证法，编成一本书。直到1980年，美国《数学老师》月刊还登载了这个定理的研究现状，随后又收到了20360百科00多封来信，增补了20多种证法并收到了一个最简单的直接证法。经过几代人的努力，100多年的很未断己粉研究，"斯坦纳-雷米欧斯"定理已成为数学百花园中最惹人喜爱的瑰丽花朵