安可林文章网新闻资讯图与网路分析
运筹学中把一些研究对象用节点表示，对象之间的关係用连线边表示。用点、边的集合构成图。图论是研究有节点和边所组成图形的数学理论和方法。图是网路分析的基础，根据具体研究的网路对象（如：铁路网、电力网、通信网等），赋予图中各边某个具体的参数，如时间、流量、费用、距离等，规定图中各节点代表具体网路中任何一种流动的起点，中转点或终点，然后利用图论方法来研究各类网路结构和流量的最佳化分析。网路分析还包括利用网路图形来描述一响工程中各项作业的进度和结构关係，以便对工程进度进行最佳化控制。
基本介绍
- 中文名：图与网路分析
- 外文名：Graph and network analysis
- 领域：运筹学
- 关係：图是网路分析的基础
- 举例：铁路网、电力网、通信网等
- 相关名词：网路最短路问题
图论介绍
运筹学中把一些研究对象用节点表示，对象之间的关係用连线边表示。用点、边的集合构成图。图论是研究有节点和边所组成图形的数学理论和方法。图是网路分析的基础，根据具体研究的网路对象（如：铁路网、电力网、通信网等），赋予图中各边某个具体的参数，如时间、流量、费用、距离等，规定图中各节点代表具体网路中任何一种流动的起点，中转点或终点，然后利用图论方法来研究各类网路结构和流量的最佳化分析。网路分析还包括利用网路图形来描述一响工程中各项作业的进度和结构关係，以便对工程进度进行最佳化控制。
图的基本概念
图是由点和点与点之间的连线组成。
若点与点之间的连线没有方向，称为边，由此构成的图为无向图。记为：G=（V，E）其中V是G的点的集合，E为G的边的集合，连线
，
的边记为
。
若点与点之间的连线有方向，称为弧，由此构成的图为有向图。记为：D=（V，A），其中V是G的点的集合，A为G的弧的集合，一条方向为从 指向 的弧记为
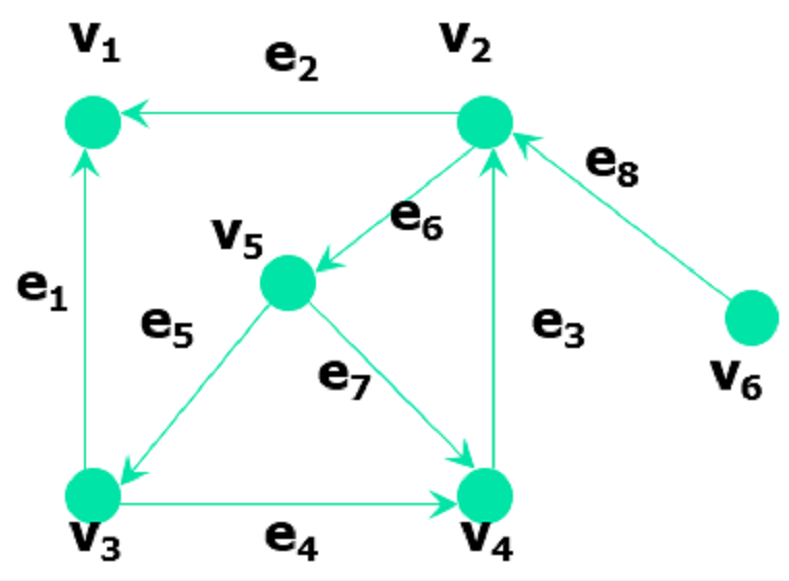
相邻点：两点之间的边属于E；
相邻边：如果两条边有一个公共端点；
环：边的两个端点相同；
多重边(平行边)：两个点之间有多于一条边(弧)；
多重图: 无环但允许有多重边的图；
简单图：无环且无多重边的图；
注：在有向图中，如果两点之间有不同方向的两条弧，不是多重边。
端点的次d(v)：点 v 作为端点的边的个数；
奇点：d(v)=奇数； 偶点：d(v)=偶数；
悬挂点：d(v)=1；悬挂边：与悬挂点连线的边，
孤立点：d(v)=0；空图：
，无边图。
在有向图中，以 为始点的边数称为 的出次，以 为终点的边数称为 的入次，入次和出次的和称为该点的次。
有向图中所有顶点的入次之和等于所有顶点的的出次之和。
图的连通性
通路：由两两相邻的点及其相关联的边构成的点边序列。如：
v0 , e1 , v1 , e2 , v2 , e3 , v3 , … , vn-1 , en , vn ,v0 , vn
分别为链的起点和终点。
简单链：链中所含的边均不相同。
初等链：链中所含的点均不相同，也称通路。
圈：起点和终点相同的链。
迴路：通路的起点和终点相同
连通图：图中任意两点之间均至少有一条链相连，否则称作不连通图。
任何一个不连通的图都可以分为若干个连同子图，每一个都称为原图的一个分图。
连通是一个很重要的概念，如果一个问题所对应的图是一个不连通图，则该问题一定可以分解成互不相关的子问题来加以研究，即可以把不连通图分解成连通的子图来研究。
树与部分树
一个没有圈的图称为一个无圈图或称为林。
一个连通的无圈图则称为树，一个林的每个连通子图都是一个树。
若T是图G=(V，E)的部分图，且T是树，则称T为G的部分树。
若T是图G的部分树，则从G中去掉T中所有的边，所得到的子图称为G中的T的余树，也称为G的一个余树。
余树不一定是树！
网路
点和边带有某种数量指标的图称为网路，或称为赋权图。
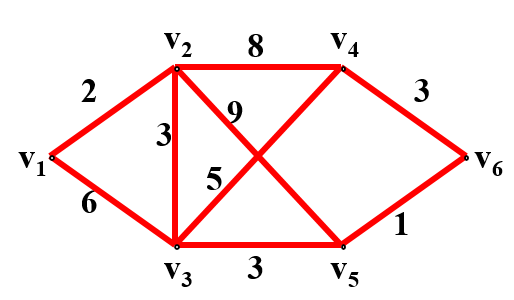
网路最小树问题
最小树问题：选取网路中的部分图，使得网路连通，且使总权数最小。
在实际套用中，经常碰到需要求一个赋权连通图的最小树的问题。例如，用节点表示城市，用边表示可以在两个城市之间架设光缆，边上的权表示光缆的长度，试求应如何架设光缆，才能使任意两城市之间均由光缆相通，且使光缆的总长度最短。
求最小树的方法，依据的是树的特点，即无圈和连通，加上最短的要求，方法主要有两种：一种称为破圈法，一种称为取边避圈法。
（1）取边避圈法 ：
方法步骤：依次在图中取一个权值最小的边，或者是相对最短的边，并且在每次取边时都不能与已取的边构成圈。
- 首先在图中选最短的边，并且将与之关联的两个点标记△；
- 然后每次都在标记点和未标记点间可能的边中取一个最短的边，并将新选的边标记；
- 重複上述过程，直到所有的点均被标记了。
（2）破圈法：
方法步骤：
- 在网路图中寻找一个圈，若已经无圈则转步骤3。
- 在圈中选取权数最大的边，从网路图中截去该边，对新的网路，转步骤1。
- 若q=p-1(边数=定点数-1)，则已找到最小树，否则网路图不连通，无最小树。
最短路问题
基本概念
网路：对有向图D=(V，A)，如果对于有向图D中的每一条弧
，都有一个数
与它对应，此时称D为一个网路，或称赋权有向图。
有向网路：网路中每个边都是有向边；
无向网路：网路中每个边都是无向边；
混合网路：网路中既有有向边，又有无向边；
网路最短路线问题：寻找网路中从起点
到终点
的最短路线。
一般的最短路问题描述
给定一个赋权有向图D=(V，A)，对每一个弧
，相应地有权
，又给定D中的任何两个顶点
和
，设P是从 到 的路，定义路P的权是P中所有弧之和，记为
，最短路问题就是要在所有从 到 的路中，求一条权最小的路，即一条从 到 的路
使得：
路 的权称为从 到 的距离，记为
。
有向图权值非负---- Dijkstra算法
Dijkstra算法的基本步骤(权值非负)
1.给顶点
标号(0)， 称为已标号点，记标号点集为
；
2.在未标号点集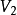
中找出与标号点集
中的顶点
有弧相连(并且以 为起点)的点
；
3.在第2步选出的点中，选出满足下麵条件的点
，并给 标号
，其中l为第一标号，
为第二标号。
4.若最后一个顶点
未标号，则转回第2步；若 已标号，则从 开始，按照第一个标号逆向追蹤，直到 ，就得到从 到 的最短路， 的第二个标号表示最短路的长度。
最大流问题
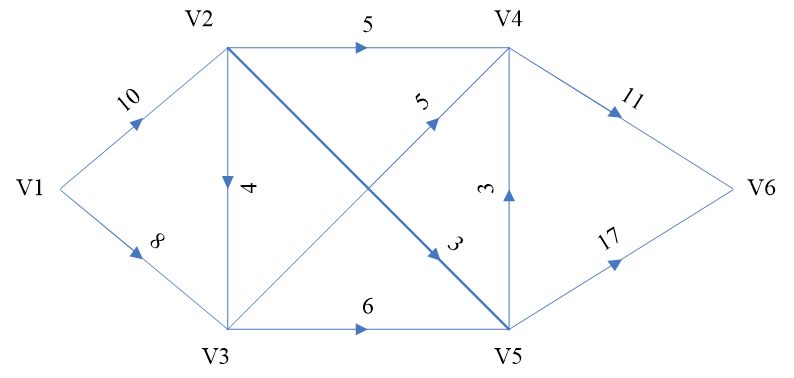
下图表示从产地 到销地
的交通网，弧旁边的数字表示这条运输线的最大通过能力，产品经过这个交通网从 运到 ，要求制定一个运输方案使得从 运到 的产品数量最多。
基本概念
网路与流：
对有向图D=(V，A)，如果其中指定某一点
为发点，另一点
为收点，其他点则称为中间点。若对于有向图D中的每一条弧 ，都有一个数
与它对应，称c为弧的容量，记为D=(V,A,C)。
寻找最大流的标号法
网路D中的点分为两类，一类是标号点(属于
)，一类是非标号点(不属于 ) ；
标号点有两类一类是已检查的，一类是未检查的。每个标号点有两个标号：第一个标号表示这个点的标号是从哪一点得到的，以便进一步找出增广链，第二个标号是用来表示方向。
1.确定初始可行流
根据图中弧的容量限制，确定一个初始的可行流，可以取零流。
2.标号过程
开始：由于始点 一定属于 ，先给始点 标上
，此时 是标号但是未检查的点，其他点都是未标号的点，选择标号但是未检查的点
，对于一切未标号的点
，若在弧 上，
，则给标号
，则变为标号但是未检查的点，否则不标号。若在弧上，
，则给标号
，则变为标号但是未检查的点，否则不标号。
重複以上步骤，一旦
被标上号就得到了一条从到的增广链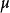
，转入调整过程。
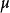
如果所有的标号都是已经检查过的，但是标号过程无法进行下去，算法结束，此时的可行流就是最大流。