
有界性
函式的有界性定义:若存在两个常数m和M,使函式y=f(x),x∈D 满足m≤f(x)≤M,x∈D 。 则称函式y=f(x)在D有界,其中m是它的下界,M是它的上界。
基本介绍
- 中文名:有界性
- 外文名:boundedness
- 所属学科:数理科学函式
- 分类:上界、下界
- 相关概念:有界、无界、
定义
定义1
设函式 在数集
在数集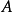 上有定义,如果存在常数
上有定义,如果存在常数 ,使得对任意
,使得对任意 ,有
,有

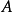



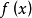
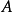
例如,函式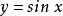 在其定义域
在其定义域 内有界,这是因为对任意
内有界,这是因为对任意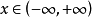 ,总有
,总有 。
。
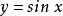

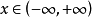

再如,函式 在其定义域
在其定义域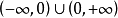 内是无界的,这是因为对任意的实数
内是无界的,这是因为对任意的实数 ,总存在点
,总存在点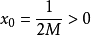 ,显然
,显然 ,使得
,使得 ,然而,对任意实数
,然而,对任意实数 ,函式
,函式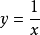 在定义域的子集
在定义域的子集 上却是有界的,这是因为对任意
上却是有界的,这是因为对任意 ,总有
,总有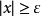 ,于是便可取实数
,于是便可取实数 .使得
.使得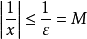 。
。

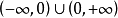

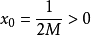



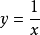


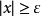

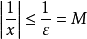
定义2
设函式 在数集
在数集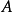 上有定义,如果存在常数
上有定义,如果存在常数 ,使得对任意
,使得对任意 ,有
,有

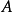




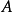




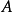

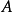
显然,若 在A上有界,则
在A上有界,则 在A必有上、下界。反之,若
在A必有上、下界。反之,若 在A上有上、下界,则
在A上有上、下界,则 在A上必有界.
在A上必有界.




由定义1可知,在集合A上有界函式 的图形在A上,应介于平行于x轴的两条直线
的图形在A上,应介于平行于x轴的两条直线 之间,如图1所示.
之间,如图1所示.


 图1
图1注意点
关于函式的有界性.应注意以下两点:
(1)函式在某区间上不是有界就是无界,二者必属其一;
(2)从几何学的角度很容易判别一个函式是否有界(见图2).如果找不到两条与x轴平行的直线使得函式的图形介于它们之间,那幺函式一定是无界的,如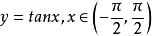 。
。
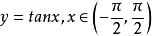
 图2
图2例题解析
例1: 讨论下列函式的有界性:
(1) ;
;

(2) .
.

解: (1)由于对一切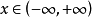 ,都有
,都有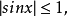 故
故 在
在 上是有界函式。
上是有界函式。
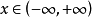
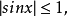


(2)根据 的图形(见图3)容易看出,不论正数M多幺大,不等式
的图形(见图3)容易看出,不论正数M多幺大,不等式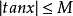 不可能对一切
不可能对一切 均成立,因此
均成立,因此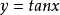 在
在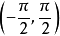 上是无界函式。
上是无界函式。

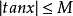

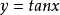
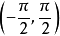
但如果在区间 上讨论函式
上讨论函式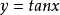 ,因对一切
,因对一切 ,不等式
,不等式 成立,故
成立,故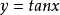 在区间
在区间 上是有界函式。
上是有界函式。

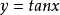


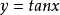

例2:
证明:函式 是有界函式。
是有界函式。

证明: 的定义域为
的定义域为 ,又
,又




 安可林文章网新闻资讯
安可林文章网新闻资讯