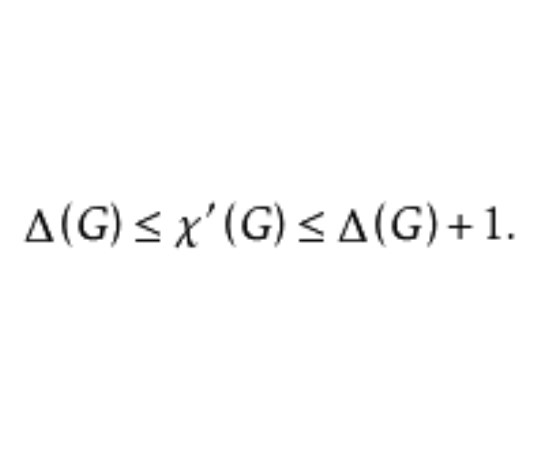
维津定理
维津定理(Vizing theorem)是关于图的边着色的一个定理,若G是简单图,则Δ≤χ′(G)≤Δ+1,其中,Δ表示G上次最大的节点的次,χ′(G)表示边色数。这个定理是维津(V.G.Vizing)于1964年发表的,由此可以将简单图分为二类:对任意简单图G,若χ′(G)=Δ,则称G为第1类图;否则,称G为第2类图。
基本介绍
- 中文名:维津定理
- 外文名:Vizing theorem
- 所属学科:数学
- 所属问题:组合学(图与超图)
- 简介:关于图的边着色的一个定理
- 提出者:维津(V.G.Vizing)
基本介绍
定理(维津1964) 任何一个图G的边色数满足:

维津定理的证明
证明对图G的边数 进行归纳证明。如果
进行归纳证明。如果 ,结论自然成立,现在假定
,结论自然成立,现在假定 ,而且结论对于边数较少的图均成立,现在考虑边数为
,而且结论对于边数较少的图均成立,现在考虑边数为 的图G,以下我们对于
的图G,以下我们对于 -边染色简称为染色,而凡是具有颜色α的边称为α-边。
-边染色简称为染色,而凡是具有颜色α的边称为α-边。





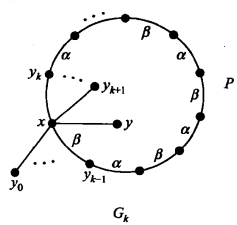 图1
图1对于任何一条边 ,根据归纳假设,G-e有一个染色.在这样一个染色中,每一个节点v处至多使用了Δ种颜色,因而有一种颜色
,根据归纳假设,G-e有一个染色.在这样一个染色中,每一个节点v处至多使用了Δ种颜色,因而有一种颜色 在v处不出现,对于任何其他一种颜色α,存在唯一一个起点是v的极大的
在v处不出现,对于任何其他一种颜色α,存在唯一一个起点是v的极大的 交错路(注意:这个路可能退化成一个节点),我们称其为发自v的
交错路(注意:这个路可能退化成一个节点),我们称其为发自v的 交错路。
交错路。




假设G没有染色,那幺有下列结论成立:
对于任意边 和任意的
和任意的 的染色,使得α在x处不出现且β在y处不出现,则α一定在y处出现,同时β一定在x处出现,而且这发自y的唯一一条
的染色,使得α在x处不出现且β在y处不出现,则α一定在y处出现,同时β一定在x处出现,而且这发自y的唯一一条 交错路一定在x处结束。
交错路一定在x处结束。



否则,我们沿着这条 交错路互换α与β的颜色后,可以得到G的一个正常Δ-边染色,与假定相违。
交错路互换α与β的颜色后,可以得到G的一个正常Δ-边染色,与假定相违。

如图1,设 是一条边,由归纳假定,
是一条边,由归纳假定, 具有一个染色(正常Δ-边染色)c0。设α为一种在x处不出现的颜色。进一步,设
具有一个染色(正常Δ-边染色)c0。设α为一种在x处不出现的颜色。进一步,设 是一个与x相关联的极大节点序列,使得
是一个与x相关联的极大节点序列,使得 是c0中在
是c0中在 处不出现的颜色,
处不出现的颜色, .对于每个图
.对于每个图 ,我们可以定义一个染色ci如下:
,我们可以定义一个染色ci如下:







如果 ,且
,且 ,则
,则 ;否则,
;否则, 。
。




注意:在每一个这样的染色ci中,x处不出现的颜色与c0的相同。
现在,设β为c0中在yk处不出现的颜色。显然,β在ck中也在yk处不出现,如果β也在x处不出现,我们可以用β给边 染色,从而将ck扩张成为G的一个染色,因此,在每一个染色中,x处都有一个β色边与之关联。由k的极大性,存在一个数
染色,从而将ck扩张成为G的一个染色,因此,在每一个染色中,x处都有一个β色边与之关联。由k的极大性,存在一个数 ,使得
,使得 。
。



设P为(ck中)Gk的一条发自yk的 -路,由于α不在x处出现,由前面的结论,P必定在x处结束,且与x关联的边色是α,由于
-路,由于α不在x处出现,由前面的结论,P必定在x处结束,且与x关联的边色是α,由于 ,这一条α就是边
,这一条α就是边 。然而,在c0和
。然而,在c0和 中,(由β的定义和
中,(由β的定义和 的定义知)β不在
的定义知)β不在 处出现,我们考虑(
处出现,我们考虑( 中)
中) 的发自
的发自 的
的 -路P',由于P'是唯一被决定的,它发自
-路P',由于P'是唯一被决定的,它发自 ,注意到P上从x到yk之间的边上
,注意到P上从x到yk之间的边上 与ck的染色相同,但是在c0中,因此也在
与ck的染色相同,但是在c0中,因此也在 中,(由β的定义知)不存在β-边,因此,P'又要在yk处结束,与前面的结论相违。
中,(由β的定义知)不存在β-边,因此,P'又要在yk处结束,与前面的结论相违。













维津定理的意义
维津定理的意义在于,根据边染色规则,所有的有限图被划分成为两部分:如果 ,则图是第一类的;否则,是第二类的。怎样判定一个图的类型一直是染色理论中的一个基本问题,任何一类非平凡图类的发现都是很不容易的,目前所知道的基本结论是悲观的,因为人们已经知道这样的判定问题是NP-困难的,不过人们仍然在发现一些非平凡的图类。
,则图是第一类的;否则,是第二类的。怎样判定一个图的类型一直是染色理论中的一个基本问题,任何一类非平凡图类的发现都是很不容易的,目前所知道的基本结论是悲观的,因为人们已经知道这样的判定问题是NP-困难的,不过人们仍然在发现一些非平凡的图类。

 安可林文章网新闻资讯
安可林文章网新闻资讯