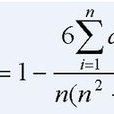
秩相关係数
秩相关係数(Coefficient of Rank Correlation),又称等级相关係数,是将两要素的样本值按数据的大小顺序排列位次,以各要素样本值的位次代替实际数据而求得的一种统计量。它是反映等级相关程度的统计分析指标,常用的等级相关分析方法有Spearman相关係数和Kendall相关係数等。
基本介绍
- 中文名:秩相关係数
- 外文名:Coefficient of Rank Correlation
- 定义:反映等级相关程度的统计分析指标
- 别称:等级相关係数
- 学科:统计学
简介
秩相关係数,亦称为“等级相关係数”,是反映等级相关程度的统计分析指标。常用的等级相关分析方法有Spearman相关係数和等。
如果秩相关係数为正,则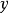 随着
随着 的增加而增加;如果秩相关係数为负,则
的增加而增加;如果秩相关係数为负,则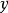 随着
随着 的增加而减小;如果秩相关係数为0,则表示随着
的增加而减小;如果秩相关係数为0,则表示随着 的增加,
的增加,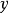 没有增大或减小的趋势。当
没有增大或减小的趋势。当 和
和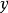 越来越接近严格单调的函式关係时,秩相关係数在数值上就越来越大。当秩相关係数为1或者-1时,就表明
越来越接近严格单调的函式关係时,秩相关係数在数值上就越来越大。当秩相关係数为1或者-1时,就表明 和
和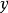 之间严格单调增加或者严格单调减小。
之间严格单调增加或者严格单调减小。
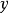

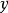


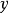

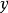

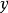
在实际套用中,有时获得的原始资料没有具体的数据表现,只能用等级来描述某种现象,要分析现象之间的相关关係,就只能用秩相关係数。
计算方法
秩相关係数的计算步骤如下:
1)把数量标誌和品质标誌的具体表现按等级次序编号;
2)按顺序求出两个标誌的每对等级编号的差;
3)按下式计算相关係数:
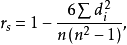
其中:秩相关係数记为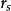 ,
,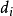 为两变数每一对样本的等级之差,即变数
为两变数每一对样本的等级之差,即变数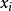 与
与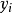 的差值,
的差值, 为样本容量。
为样本容量。
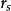
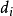
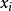
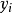

秩相关係数与相关係数一样,取值-1到+1之间,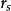 为正时表示正相关,
为正时表示正相关,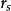 为负时表示负相关,
为负时表示负相关,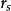 等于零时表示相关为零。但与相关係数不同的是,它是建立在等级的基础上计算的,较适用于反映序列变数的相关。
等于零时表示相关为零。但与相关係数不同的是,它是建立在等级的基础上计算的,较适用于反映序列变数的相关。
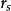
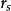
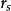
示例
例如,2003年中国大陆各省(直辖市、自治区)的GDP( )和总人口(
)和总人口(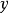 )数据及其位次,可以计算出来,将相应数据代入公式,就可以计算它们之间的秩相关係数。
)数据及其位次,可以计算出来,将相应数据代入公式,就可以计算它们之间的秩相关係数。

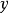
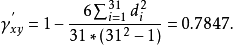

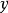
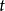
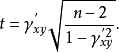
相关检验
将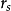 的绝对值同spearman相关係数统计表中的临界值
的绝对值同spearman相关係数统计表中的临界值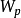 进行比较。如果
进行比较。如果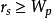 ,则表明变化趋势有显着意义;如果
,则表明变化趋势有显着意义;如果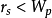 ,则表明变化趋势没有显着意义;如果
,则表明变化趋势没有显着意义;如果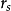 为正值,则表明有上升趋势;如果
为正值,则表明有上升趋势;如果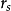 为负值,则表明有下降趋势。秩相关係数
为负值,则表明有下降趋势。秩相关係数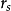 检验的临界值表如下:
检验的临界值表如下:
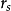
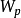
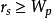
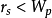
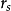
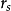
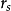
表1.秩相关係数检验的临界值表
n | 显着水平α | 显着水平α | n | 显着水平α | 显着水平α |
0.05 | 0.01 | 0.05 | 0.01 | ||
4 | 1.000 | -- | 16 | 0.425 | 0.601 |
5 | 0.900 | 1.000 | 18 | 0.399 | 0.564 |
6 | 0.829 | 0.943 | 20 | 0.377 | 0.534 |
7 | 0.714 | 0.893 | 22 | 0.359 | 0.508 |
8 | 0.643 | 0.833 | 24 | 0.343 | 0.485 |
9 | 0.600 | 0.783 | 26 | 0.329 | 0.465 |
10 | 0.564 | 0.746 | 28 | 0.317 | 0.448 |
12 | 0.456 | 0.712 | 30 | 0.306 | 0.432 |
14 | 0.456 | 0.645 | -- | -- | -- |
注: 代表样本个数,
代表样本个数,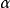 代表不同的置信水平,也称显着性水平,表中的数值为临界值 。
代表不同的置信水平,也称显着性水平,表中的数值为临界值 。

 安可林文章网新闻资讯
安可林文章网新闻资讯