安可林文章网新闻资讯
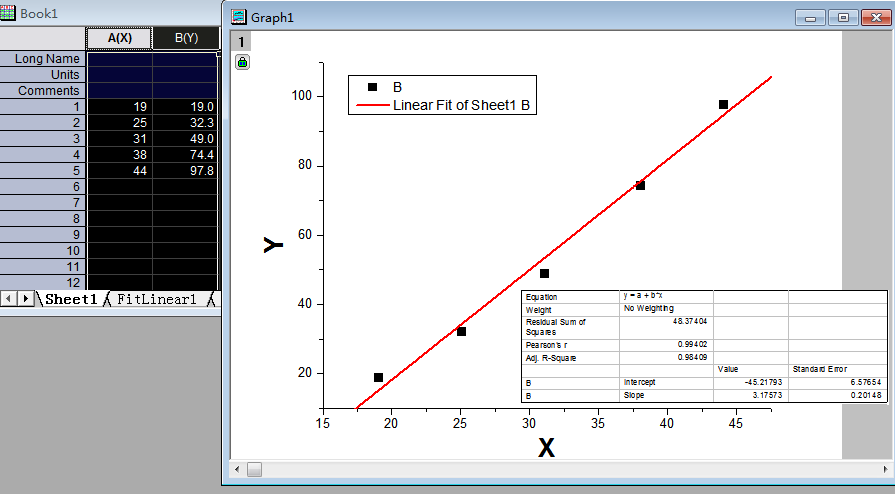
线性关係
两个变数之间存在一次方函式关係，就称它们之间存线上性关係。正比例关係是线性关係中的特例，反比例关係不是线性关係。更通俗一点讲，如果把这两个变数分别作为点的横坐标与纵坐标，其图象是平面上的一条直线，则这两个变数之间的关係就是线性关係。即如果可以用一个二元一次方程来表达两个变数之间关係的话，这两个变数之间的关係称为线性关係，因而，二元一次方程也称为线性方程。推而广之，含有n个变数的一次方程，也称为n元线性方程，不过这已经与直线没有什幺关係了。
基本介绍
- 中文名：线性关係
- 外文名：linear relation
- 别名：正比例关係
- 基本表达式：y=kx+b (k，b为常数)
- 所属领域：数理科学
- 反义词：非线性关係
一般定义
线性关係的显着特徵是图像为过原点的直线(没有常数项的情况下，如：y=kx+jz,（k,j为常数，x,z为变数)；而当图像为不过原点的直线时，函式称为直线关係。
线性关係与直线关係是两不同的，经常被大家搞混淆。
首先每一项（常数项除外）的次数必须是一次的（这是最重要的）
如：x=y+z+c+v+b
那幺就说他们（x与y,z,c,v,b都是变数）是线性关係，可以说成：x与y是线性关係，或y与z是线性关係等等，
如果出现平方，开方这些就肯定不是线性关係
如果每项的次数不是一次就不是线性关係：x=y*z（这里假定y,z是变数而不是常数），那幺x与y,或x与z就不是线性关係，
常数对是否构成直线关係没影响（假定常数不为0）如：x=k*y+l*z+a（k，l是常数，y，z是变数，a是常数）那幺x与y,z还是线性的，因为项：k*y是一次的，l*z这项也是一次的，常数项a没影响.
如：x=7*y+8*z是线性的，x=－y－2*z是线性的。x=2*y*z是非线性的（因为2yz这一项不是一次的），
从二维图像来讲（假定只有y跟x这两个变数），线性的方程一定是直线的，曲的不行，有转折的也不行。
向量的线性表示
给定向量组A：α1，α2，…αn，伐以及向量b，若存在一组数k1，k2，…，kn，使得
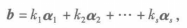向量的线性关係则称向量b可由向量组A线性表示，也称向量b是向量组A的一个线性组合，k1，k2，…，kn称为这个线性组合的係数．
向量b可由向量组A线性表示，也就是线性方程组
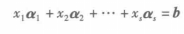向量的线性关係有解．
设有向量组A：α1，α2，…αn，和B：β1，β2，…，βn，若向量组B中的每一个向量都可由向量组A线性表示，则称向量组B可由向量组A线性表示；如果向量组A和向量组B能互相线性表示，则称这两个向量组等价，记作A≌B．