线性(数学概念)

定义

卷积(Convolution)既是一个由含参变数的无穷积分定义的函式，又代表一种运算。其运算性质线上性系统理论、光学成像理论和傅立叶变换及其套用中经常用到。

卷积的运算性质有线性特性，複函数的卷积，可分离变数，卷积符合交换律，卷积符合结合律，坐标缩放性质，卷积位移不变性，函式f（x，y）与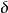

函式的卷积。

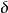
其中线性特性可描述为：

设a，b为任意常数，则对于函式f(z，y)，h(x，y)和g(x，y)，

{af(x，Y)+bh(z，y)}*g(z，y)=-af(x，y)*g(x，y)+bh(x，y)*g(z，y)。

同样有：

f(x，y)*{ah(x，y)+bg(x，y)=af(x，y)*h(x，y)+bf(x，y)*g(x，y) 。

卷积运算是线性时不变系统分析的重要工具，很多滤波器的设计中都要用到卷积运算。下面给出线性卷积运算的定义。设有离散信号x(n)和y(n)，其线性卷积为：

。

与线性相关运算不同的是：

①卷积运算时，y（n）要先反折得到y(-n)。

②m>0表示y(-n)序列右移，m<0表示左移，不同的m得到不同的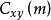

值。其余与相关计算相同。线性卷积运算的简洁表示为：

。

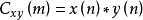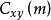
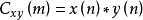
式中的

表示线性卷机运算符。

令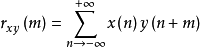

与

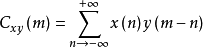相比较，

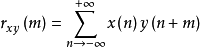
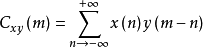
则有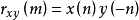

。

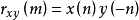
因而线性卷积运算结果序列点长也是序列x(n)的长度加上y(n)长度再减去1。

再令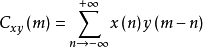

中k=m—n，则n=m-k，

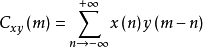
得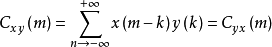

。

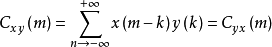
因而卷积运算交换先后不影响结果。