它是定常系统的特例，但只要在所考察的範围内定常系统的非线性对系统运动的变化过程影响不大，那幺这个定常系统就可看作是线性定常系统。对于线性定常系统，不管输入在哪一时刻加入，只要输入的波形是一样的，则系统输出回响的波形也总是同样的。线性定常系统的分析和设计均比时变系统或非线性系统容易得多，是自动控制理论中最成熟的部分。

系统对输入信号导数的回响，可以通过系统对该输入信号回响的导数来求得；而系统对输入信号积分的回响，可以通过系统对该输入信号回响的积分来求取，其积分常数有初始条件确定。如：单位脉冲、单位阶跃和单位速度输入信号存在微分和积分的关係，其一阶惯性环节的单位脉冲回响、单位阶跃回响和单位速度回响之间也存在着同样的微分和积分关係。

系统稳态输出和输入的频率相同，但输出和输入的振幅比（幅频特性）、相位差（相频特性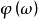）都是频率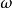的函式。换言之，在波形图上输出与输入和横轴交点间距一致，但波形高度不同且波形有平移。

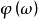
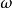
用数学式表达：若输入信号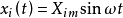， 则有输出信号。

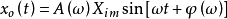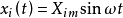
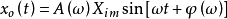
式中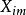：——正弦输入信号的振幅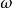——正弦输入信号的频率

系统稳定性分析主要是时域和频域上的分析，具体地讲包括劳斯判据、赫尔维茨判据、奈奎斯特判据（奈氏图）、对数判据（伯德图）、根轨迹法等。其中前两者属于代数判据，后三者需作图再判断系统稳定性。