一阶保持（Frst-order hold、FOH）是一种重建信号的数学模型，可以透过传统的数位类比转换器（DAC）及称为积分器的模拟电路完成。一阶保持可以将讯号重建为分段线性近似原始讯号的函式。在实务上，像一阶保持或零阶保持之类的保持电路有其必要性。根据採样定理，可以将离散后的讯号用狄拉克δ脉冲序列x_s(t)表示，再经过低通滤波器即可还原到原始的讯号。不过实务上无法输出狄拉克δ脉冲序列。利用传统的数位类比转换器以及一些线性类比电路就可以重建预测型或是延迟型的一阶保持电路。

虽然在实务上的作法有所不同，但可以将假想的狄拉克δ脉冲序列x_s(t)有特定特性的滤波器（若是线性时不变系统，可以用冲激回响完全描述其特性），因此每一个脉冲输入都可以产生正确的分段线性输出。

一阶保持是利用假想的滤波器或是线性时不变系统，将理想的取样讯号

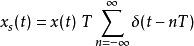
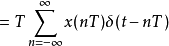
转换为分段线性的讯号。

所得到的等效冲激回响为

其中 是三角形函式。等效频率回响是冲激回响的傅立叶变换

其中 是正规化的Sinc函式。可以令s=i2 πf，得到FOH传递函式的拉普拉斯变换：

因为一阶保持滤波器的冲激回响在t小于0时就已有值，因此此系统是反因果系统。

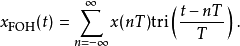
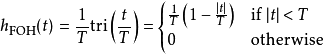
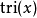
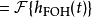
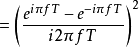
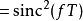
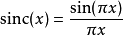
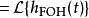
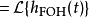
延迟一阶保持（Delayed first-order hold）有时也称为因果一阶保持（causal first-order hold）和一阶保持相同，但输出会延迟一个取样周期才输出，因此会有延迟的分段连续信号

其等效冲激回响为

其中 为三角形函式。等效频率回响是冲激回响的傅立叶变换

可以令s=i2 πf，得到FOH传递函式的拉普拉斯变换：

延迟一阶保持为因果系统。冲激回响在t小于0时没有值。这类的延迟一阶保持可以用增益为H(z) = 1 −z的数字滤波器，将数字滤波器（x[n]−x[n−1]）的输出送到传统的数位类比转换器（本质上是零阶保持），再用H(s) = 1/(sT)来积分DAC的输出。

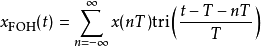
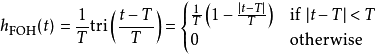
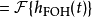
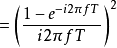
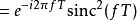
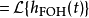
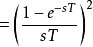
预测型一阶保持（predictive first-order hold）和上二一个一阶保持的差异较大，预测型一阶保持是因果系统的假想线性时不变系统，可以将理论取样信号

转换为分段线性输出信号，会用目前取样以及上一次的取様来线性外推下一个取样点，此滤波器的输出为

其等效冲激回响为

其中为rect(x)矩形函式，而tri(x)为三角形函式。

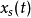
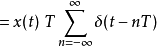
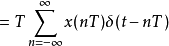
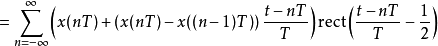
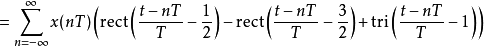
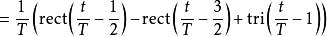
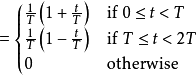
等效频率回响为冲激回响的傅立叶变换。

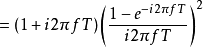
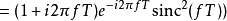
其中sinc(x)为Sinc函式。可以令s = i 2 π f，得到FOH传递函式的拉普拉斯变换：

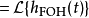
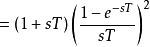
此为因果系统。预测型一阶保持的冲激回响不会在输入脉冲之前就出现。这种分段线性的重建信号方式可以用增益H(z) = 1 −z。