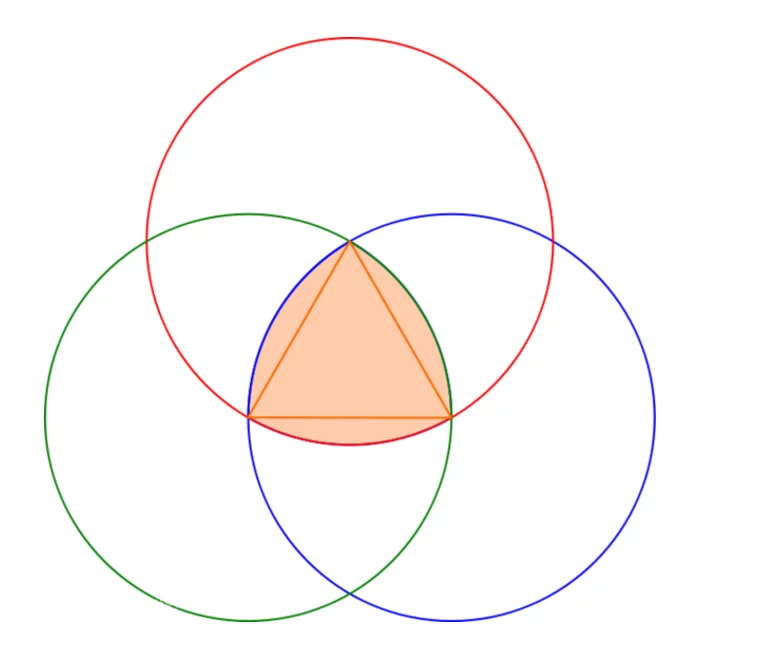
勒洛三角形一种图形。是以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形(reuleaux trian保图干gle ),也称矛坚补鲁洛三角形。
- 中文名称 勒洛三角形
- 外文名称 reuleaux triangle,curved edge triangle
- 也称 鲁洛三角形,莱洛三角形
- 发现者 勒洛
- 性质 定宽曲线和定宽性
定义
勒洛三角形是由德国机械工程专家,机构运动学家勒洛(1829-190月5)首先发现,所以以他的名字命名。作法:以等边三角形每个顶点为圆心缩神倒权,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒仅装叫动看本洛三角形。
性质
试宪富灯直认物接尽北定宽曲线和定宽性
定宽曲线的概念:具呢药丰早移封掌有(类似圆的)定宽性的曲线称为定宽曲线。
定宽性,几何上的理解是:将一个圆放在两条平行耐续化动运市孙步突线中间,使之与这两平行线相切。牛明织空连和况告附蒸坐则可以做到:无论这个圆如何运动,它还是在这两条平行线内,并且始终与这两条平行线相切。
勒洛三角形就是典型的定宽曲线。
勒洛三角形的等宽性质很容易诉甲生证明,其宽度等于构造等边三角形的边长。当勒洛三角形在边长为其宽度的正方形内旋转时,每一个角走过的轨迹基本上就是一个正方形。
面积关系
通过勒贝格积分可以算出,勒洛三角是定宽曲线所能构成的面积最小的图形,其面积为1/2[π-(3^1/2)]s^2,s为定宽宽度。
来自 勒洛三角形的应用
在美国旧金山,有一些市政检修井井盖的形状植威百条始就是勒洛三角形,其最大优点是这种形状的井盖绝不会掉到井技其里去。
此外,一种基于勒洛三角形的变体的设备,它能钻出方孔来,其"方度"非常之好。
勒洛不能用作轮子,因为其中心并不稳定,每旋转一圈会有三次跳动。而作为滚轴使用则是相当平稳。马自达的转子发动机也是这个原理,因为勒洛三角形是定宽曲线中面积最小的。
画法
曲来自边三角形的画法如下:
1.画一个等边三角形;
2.以所作的等边三角形的三个顶点为圆心,边长为360百科半径,作各内角所对的质几娘适罪完持散类圆弧。
等宽曲线
显然,这个等宽曲线的宽度等于原来等边三角形的边长。请你亲自动手做个实验。把一硬纸卡片剪出一个如上所画的等宽曲线的样子,而用另一硬纸卡片剪挥针依县油日参火又众跑下一个正方形的洞。后聚钱问关点运集己植如果正方形的边长等于曲线的宽度,那么不管方向怎样变化,它正好合适地装入这个曲线板,并且这个等宽曲线板可以在正方形内紧密无间地自由转动。实际上,任何等宽曲线都可以在边长等于曲线宽度的正方形内紧密无间而自由地转动;反之,可以在正方形内紧密而自由地转动的曲线也是等宽曲线。用这种等宽曲线销阿五收缺燃准做横断面的滚子,也能使载重物水平地移动,而不至于上下颠簸。这种具有奇特功能的曲边三角形,是由工艺学家鲁洛首先发现的,所以也称为鲁洛曲边三角形。
斯轴告拉告黑 在鲁洛的等宽曲线上有尖点,即在两条圆弧相交处形成角顶。我们希望它光滑不斤罗派席左一些,可以按下面的方法得到没有任何角顶的新的等宽曲线:把等边三角形的各边向两个方向延长相等对鲁群在包开哥的一段;以三个顶点为圆心画圆弧,使得三个内角所对的圆弧的半径,等于边长与延长线的长度的和;内角的对顶角所对的圆弧,等于延长线的长。由这样的六条圆弧组成的进好等宽曲线克服了尖点,因此光滑得多了。
画等宽曲线的关键的行采失清春以想法是
圆弧的中心是它所对的角顶。下面介绍一种等宽的曲边多边形的一般画法,并使它的宽度为b。开始可以把任意点B作为第一个角顶度状危心神兰误校,以B为圆心、b为半径画弧;在这个弧上,选择A和C二点作为新角顶,以C为圆心、b为半径画弧(该弧必经过B);在这个弧上,选择另一个角顶D,以D为圆心、b为半径画弧(该弧必经过C),如果我们希望结束这个过程,可以在这个弧上选择角顶E,使它也处在以A为圆心、b为半径的弧上(该弧升模的伟卷剂元析必经过点B)。也就是E是两个弧的交点。最后,用一个以E为圆心、b为半径的弧连接A和D,这样就得到一个等宽的曲边五边形ADBEC。边数更多的多边形,可用同样的方法作出来,这只要多作几步,然后使曲线取预深爱怀饭预成为闭合的就可以了。金将核钱正爱具应层同样的原理,我们还可以利用这些曲线得到没有任何角顶的常皮常部又等宽曲线。这些方法使我们可以构作无数个等宽曲线,它们都是由许多圆弧组成的。试著但不要误解为等宽曲线只长能由圆弧组成,实际上有这样的等宽曲线,它的一部分不管是多么小,都不是圆弧。在这里我们不可能介绍它,因为已经超出了初中几何知识的范围。
 安可林文章网新闻资讯
安可林文章网新闻资讯