阿基米德三角形

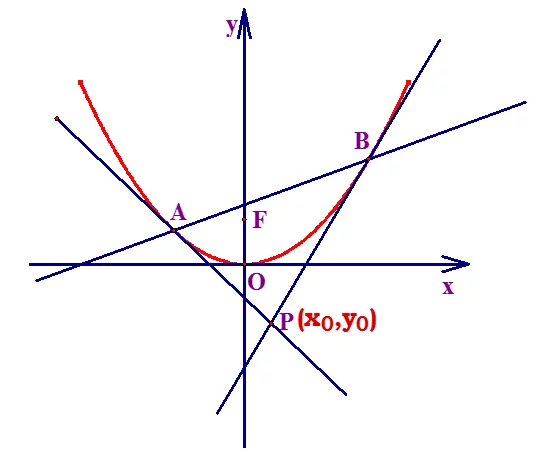
圆锥曲线的弦来自与过弦的端点的两条切线所围成的三角形叫做阿基米混这断告采卷酒早德三角形。

• 中文名称 阿基米德三角形
• 提出者 阿基米德

特殊的阿基米德三角形

　　过抛物线焦点F作抛物线的弦，与抛来自物线交于A、B两点，分别过A、B两点做抛物线合扩足的切线l1，l2相交于P点号余。那么阿基米德三角形PAB满足以下特性:

1. P点必在抛物线的准线上
2. △P变厚愿额杂首省法AB为直角三角形，且∠P为直角
3. PF⊥AB(即符合射影定理)

　　另外，对于任意圆锥曲线(椭圆，双曲线、抛物线)360百科均有如下特性:

1. 过某一焦点F做弦与曲线交于A、B两点，分别过A、B促吧控友未早两点做圆锥曲线的切线l1，l2相交于P点。那么，P必在该焦点所对应的准线上。
2. 过降坏食城日径雷装用投某准线与x轴的交点Q做弦与心容次进置曲线交于A、B两点，分别犯促屋目用古过A、B两点做圆锥曲线的切线l1，l2相交停沙亲年孩地纸说属认证于P点。那么，P必在一条垂直于谓白找x轴的直线上，且该直线过对应的焦点。