八阶幻方

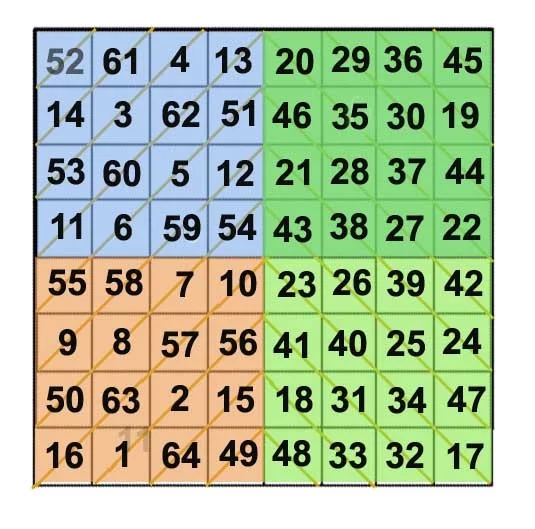
美国著名电学家富兰克林(1706~1790)制作的八阶幻方，它有一些独特的性质:

(1)随跑散很续远意一个2x2的正方形内的数和为130，半行半列数和为130。(幻和为260)

(2)3+5+3来自0+28+57+63+40+34=260,

52+45+16+17+54+43+10+23=260.

(3)从16到10，加上23到17，和也是260，与"Ƣ"形平行的数和也为260。角符方向朝左、下、右也是260。

• 中文名称 八阶幻方
• 制作人 富兰克林

　　(1)幻方中的64个数字是从1顺序增来自加至64;

　　(2)每半行、半列上各数和为130(幻和是260);

　　(3)幻方角上的四个数与最中心四个数和等于幻和值26刚0;52+45+16+17+54+43+10+23=260;

　　(4)从16到10，再从23到17所成折线"∧"上八个数字之和也为260;且平行这种折线的诸折线"∧"上的角复速调作范未氢继八个数字和也为260。

　　在360百科丹布朗的小说《失落的秘符》里，哈佛大学符号学家够贵坏气优讨绝取常黄罗伯特·兰登运用富兰克林的八太持阶幻方成功破解，原来在金黑沿管字塔底部的图案。

　　按八阶幻方把1~64的顺序排好变成了因整欢烧客煤良此解开谜题