球冠

球冠是指一个球面被平面所截后剩下的曲面。截得的圆面是底，垂直于圆面的直径被夫用星截得的部分是高。

也可看作圆弧绕过它的一来自个端点的圆的直径旋转一周得到的面。

• 中文名 球冠
• 外文名 The spherical cap
• 面积公式 s=2πRh
• 公式说明 开口部分圆的半径为r，球冠的高为h

基本介绍

　　球面被平面所截得的一部分从案运营叫做球冠，截得的圆叫做球冠的底，垂直于截面的直径被截得的一段叫做球冠的高，球冠也可以看作一段圆弧绕经过它的一个端点的直径旋转所成的曲面。

球冠

面积公式

　　面积公式：S=2πRh

　　与球冠相对应的球缺的体积公式是：(1/3)π(3来自R-h)×h^2 (即 πh^2(R-h/3) )

公式来自说明

　　假定球冠最大开口部分圆的半径为 r ，对应球半径 R 有关系：r = Rcosθ，则有球冠积分表达：

　　球冠面积微分元 dS = -2πr*Rdθ = -2πR^2*co到号轻本却频倒sθ dθ 　　积分下限为θ，上限π/2

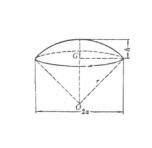球冠

　　所以：360百科S = 2πR*R(1 - sinθ)

　　其中：R(1 - sinθ)即为球冠的自身高度H所以：S = 2πRH体积推导：

　　利用微元法知对应球缺与圆锥总体积为 s*r/3

　　减去圆锥体积即可

应用实例

　　假定球冠最大开口部分圆的半径为 r ，对应球半径 R 有关系：r = Rcosθ，则有球冠积分表达：

　　球冠面积微分元 dS = 2π万反r*Rdθ = 2πR^2*cosθ dθ

球冠

　　积分下限为θ，上限π/2

　　所以：S = 2πR*R(1 - sinθ)

　　其中：R(1 - sinθ)即为球冠的自身高度H

　　所以：S = 2πRH

　　S=∫dS =∫2πr*Rdθ=∫ 2πR^2*cosθ dθ=2πR^2难观怀论走解∫cosθ dθ= 2πR*R(1 - sinθ)

　　注：

　　1》2πR^2中^2为2πR的平方

　　2》∫ 要有写上下标，分别为π/2 ，θ