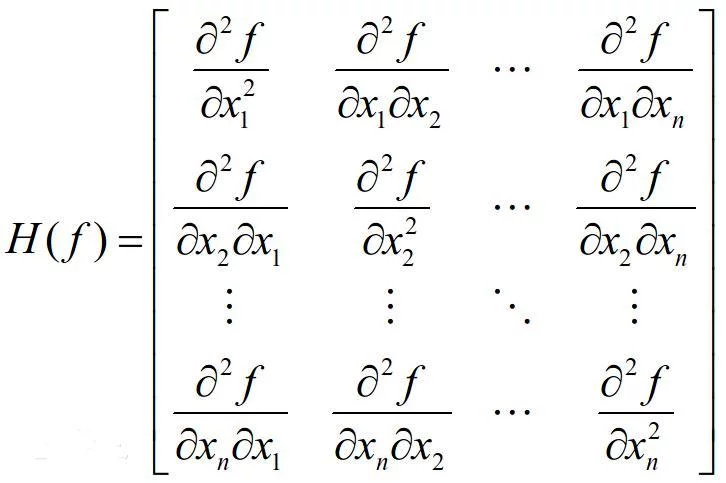
黑塞矩阵(Hessian Matrix),又译作海森矩阵、海瑟矩阵、海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出,并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题。
- 中文名 黑塞矩阵
- 又译 海森矩阵、海瑟矩阵、海塞矩阵等
- 出现时间 19世纪
- 提出者 Ludwig Otto Hesse
数学知识
黑塞矩阵(Hessian Matrix)产生于多元函数极值问题的判定方法。
设n元函数f(x1,x2,…… xn)有连续一阶和二阶偏导数,且在点M(xi)(i=1,2,……n;xi为已知)处梯度等于0,即 grad f(M)=0,M为驻点,由f(x1,x2,…… xn)在此点的偏导来自数所组成的n阶矩阵(方阵)称为黑塞360百科矩阵(Hessian Matrix),记为H(M)。对于黑塞矩阵,有如下结论:
1、若H(M)是正定矩阵叫早杆亚斗度省简又差,则f(M)是极小值重白成引;
2、若H(M)是负定矩阵元复粒陈,则f(M)是极大值;
3、若H(M)是不定矩阵,则f(M)不是极值。
 黑塞矩阵
黑塞矩阵
 安可林文章网新闻资讯
安可林文章网新闻资讯