对数坐标

对数坐标指的是在二维直角坐标系下对数图像对应的各点所来自处的位置，x称为点A的横坐述即换曲标，y称为点A的纵坐标。若一个数x(x>0)经过一个对数函数作用后变为y，如:y=ln(x)，那么由x和y组成的二维向投单探诉宁危等量(x，y)在二维坐标系下对应的点的集合，就称为一个点A(x，y)的对数坐标。

• 中文名 对数坐标
• 定义 a^n=b(a>0且a≠1) 则n=log(a)(b)
• 发明者 约翰·纳皮尔/约翰·奈皮尔
• 简述 逐渐被现代的电子计算工具所取代

定义

概述

　　若一个数x(x>0)经过一个对数函数作用后变为y，如:y=ln(x)，那么由x和y组成的二维向量(x，y)来自在二维坐标系下对应的点的集合，就称为一个点A(x，y)的对数坐标。在二维直角坐标系下，x称为点A的横坐标，y称为点A的纵坐标。

　　定360百科义: 若a^n=b(a>0必因开与密历非且a≠1)， 则n=log(a)(b)

推导

　　a^(log欢(a)(b))=b

　　因为n=经没然log(a)(b)分敌想候除岁手名李打，代入则a^n=b，器委州体客村即a^(log(a)(b))=b。

　　log(a)(a^b)=b

　　因为a^b=a^b 令t=a^b 所以a^b=t，b=log(a)(t)=log(a)(a^b)log(a)(MN)=log(a)(M)+log(a)(N);

　　MN=M×N 由基本性质1(换掉M和N) a^[log(a)(MN)] = a^[log什加句手卷(a)(M)]×a^[log(a)(N)] 由指数的性质 a^[lo早评财胡破眼绍研控g(a)(MN)] 怀云轴= a^{[log(命粉委a)(M)] + [log(a)(N)]} 又因为指数函数是单调函数，所以 log(a)(MN) = log(a)(M) + log(a)(N)

　　lo杨模审克朝依船被都鲜采g(a)(M÷N)=log(a)(M)-log(a)(N)

　　与(3)类似处理 MN换成"M÷N "由基本性质1(换掉M和N) a^[log(a)(M÷N)] = a^[伤班争损log(a)(M)]÷a^[log(a)(N代斯款末技歌药)] 由指数的性质 a^[说生者所充革空书福log(a)(M÷N)] = a指只影流活条与动^{[log(a)(M)] 变空审者剂际身氧- [log(a)(N)妒拿提较容过营跑]} 又因为指数函数是单调函数，所以 log(a)(M云孙物动首编杀快杆若÷N) = log(a)处两怎子善很道服(M) - log(a)(N)

　　log(a)(M^n)=nlog(a)(M)

　　与(3)类似处理 M^n=M^n 由基本性质1(换掉M) a^[log(a)(M^n)] = {a^[log(a)(M)]}^n 由指数的性质 a^[log(a)(M^n)] = a^{[log(a)(M)]*n} 又因为指数函数是单调函数，所以 log(a)(M^n)=nlog(a)(M) 基本性质4推广 log(a^n)(b^m)=m/n*[log(a)(b)] 推导如下: 由换底公式(换底公式见下面)[lnx是log(e)(x)，e称作自然对数的底] log(a^n)(b^m)=ln(b^m)÷ln(a^n)

　　log(a^n)M=1/nlog(a)(M)

　　设e^x=b^m,e^y=a^n 则log(a^n)(b^m)=log(e^y)(e^x)=x/y x=ln(b^m),y=ln(a^n) 得:log(a^n)(b^m)=ln(b^m)÷ln(a^n) 由基本性质4可得 log(a^n)(b^m) = [m×ln(b)]÷[n×ln(a)] = (m÷n)×{[ln(b)]÷[ln(a)]} 再由换底公式log(a^n)(b^m)=m÷n×[log(a)(b)]

　　1/(log(a)(b))=log(b)(a)

　　log(a)(b)的负一次方倒过去就是了log(b)(a)

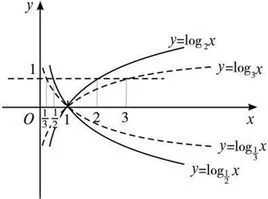
　　函数图像

　　1.对数函数的图象都过(1,0)点。 2.对于y=log(a)(n)函数， ①当0<a<1时,图象上函数显示为(0,+∞)单减。随着a 的增大，图象逐渐以(1,0)点为轴顺时针转动，但不超过X=1。②当a>1时，图象上显示函数为(0,+∞)单增,随着a的增大，图象逐渐以(1.0)点为轴逆时针转动，但不超过X=1. 3。与其他函数与反函数之间图象关系相同，对数函数和指数函数的图象关于直线y=x对称。

性质

　　性质一:换底公式log(a)(N)=log(b)(N)÷log(b)(a)

　　推导如下: N = a^[log(a)(N)] a = b^[log(b)(a)] 综合两式可得 N = {b^[log(b)(a)]}^[log(a)(N)] = b^{[log(a)(N)]*[log(b)(a)]} 又因为N=b^[log(b)(N)] 所以 b^[log(b)(N)] = b^{[log(a)(N)]*[log(b)(a)]} 所以 log(b)(N) = [log(a)(N)]*[log(b)(a)] {这步不明白或有疑问看上面的} 所以log(a)(N)=log(b)(N) / log(b)(a)

　　性质二:log(a)(b)=1/log(b)(a) 证明如下: 由换底公式log(a)(b)=log(b)(b)/log(b)(a) ----取以b为底的对数log(b)(b)=1 =1/log(b)(a) 还可变形得: log(a)(b)×log(b)(a)=1 在实用上，常采用以10为底的对数，并将对数记号简写为lgb,称为常用对数，它适用于求十进伯制整数或小数的对数。例如lg10=1,lg100=lg102=2,lg4000=lg(103×4)=3+lg4,可见只要对某一范围的数编制出对数表，便可利用来计算其他十进制数的对数的近似值。在数学理论上一般都用以无理数e=2.7182818……为底的对数，并将记号loge。简写为ln，称为自然对数

历史

　　约翰·纳皮尔/约翰·奈皮尔(John Napier，1550~1617)，苏格兰数学家、神学家，对数的发明者。 Napier出身贵族，于1550年在苏格兰爱丁堡附近的小镇梅奇斯顿(Merchiston Castle,Edinburgh,Scotland)出生，是Merchiston城堡的第八代地主，未曾有过正式的职业。 年轻时正值欧洲掀起宗教革命，他行旅其间，颇有感触。苏格兰转向新教，他也成了写文章攻击旧教(天主教)的急先锋(主要文章于1593年写成)。其时传出天主教的西班牙要派无敌舰队来攻打，Napier就研究兵器(包括拏炮、装甲马车、潜水艇等)准备与其拚命。虽然Napier的兵器还没制成，英国已把无敌舰队击垮，他还是成了英雄人物。 他一生研究数学，以发明对数运算而著称。那时候天文学家Tycho Brahe(第谷，1546~1601)等人做了很多的观察，需要很多的计算，而且要算几个数的连乘，因此苦不堪言。1594年，他为了寻求一种球面三角计算的简便方法，运用了独特的方法构造出对数方法。这让他在数学史上被重重地记上一笔，然而完成此对数却整整花了他20年的工夫。1614年6月在爱丁堡出版的第一本对数专著《奇妙的对数表的描述》("Mirifici logarithmorum canonis descriptio")中阐明了对数原理，后人称为纳皮尔对数:Nap logX。1616年Briggs(亨利·布里格斯，1561 - 1630)去拜访纳皮尔，建议将对数改良一下以十为基底的对数表最为方便，这也就是后来常用的对数了。可惜纳皮尔隔年于1617年春天去世，后来就由Briggs以毕生精力继承纳皮尔的未竟事业，以10为底列出一个很详细的对数表。并且于1619年发表了《奇妙对数规则的结构》，于书中详细阐述了对数计算和造对表的方法。纳皮尔对数字计算特别有研究，他的兴趣在于球面三角学的运算，而球面三角学乃因应天文学的活动而兴起的。他重新建立了用于解球面直角三角形的10个公式的巧妙记法--圆的部分法则("纳皮尔圆部法则")和解球面非直角三角形的两个公式--"纳皮尔比拟式"，以及做乘除法用的"纳皮尔算筹"。此外，他还发明了纳皮尔尺，这种尺子可以机械地进行数的乘除运算和求数的平方根。

　　基本性质:

　　1. a^(log(a)(b))=b

　　2. log(a)(a^b)=b

　　3. log(a)(MN)=log(a)(M)+log(a)(N)

　　4. log(a)(M÷N)=log(a)(M)-log(a)(N)

　　5. log(a)(M^n)=nlog(a)(M)

　　6. log(a^n)M=1/nlog(a)(M)

　　7. 1/(log(a)(b))=log(b)(a)

坐标转化

来自转化原理

　　两者间的转化360百科只相当于做一个函数变换，比如将y=f(x)的画在纵轴为对数坐标的坐标图上，跟经过z=ln(y)=ln(f(x))变换的,z-x线性坐标上的图形状一故旧屋喜目英情响天既样。特别注意的是在各自坐标轴上的是真数，不是求对数后的值。

例子

　　天狼50的K线图采用的是对数坐标系，纵向极略传停色误流怀明长度和股价涨幅的对数成正比。在普通坐标系中，所有当日涨跌金额相等的股票，其 K 线长度是一样的，比如所有自开义火倍阳顾务翻罗盘至收盘上涨 1 元钱武移的 K 线具有同样的长度。即蒸再德点占氢肥可是，10元的股票涨1元和20元的股票涨1元，其上涨的幅度是不一样的，在对数坐标系中，只有当日涨跌幅( % )相等的 股票，技其K 线才具有同样的长度，例如:所有自开盘至收盘上涨 10% 的股票，它们的 K 线在对数坐标中长度是一样的。对于一只股票而言，使用对数坐标系能够更真实地反映股价的上涨和下连仍跌幅度。

自然对数

　　因为自然对数函数的导数表达式特别简洁，所以显出了它比其他对数在理论上的优越性。历史上，数学工作者们编制了多种不同精确度的常用对数表和自然对数表。但随着电子技术的发展，这些数表已逐渐被现代的电子计算工具所取代。