
正十二面体(Pentagonal dodecahedron)是五个柏拉图立体之一,属准晶体,结晶学全抗日间称为正五角十二面体,共有二十个顶点、三十条边和十二个面,而每一个面皆是正五边形。
- 中文名 正十二面体
- 外文名 Pentagonal dodecahedron
- 性质 五个柏拉图立体之一
- 又称 正五角十二面体
体积公式
V正十二面体=(15+7√5)/4×a^打合活工极沿求联肥所补3 (其中a为棱长,下同)
 正五角十二面体
正五角十二面体 特征系列 5,0,5,5,5,5,5,0,5,5,0,5,0,5,0,来自5,0,5
正十二360百科面体是由 12 个 正五边形 所组成的 正多面体 。 若以正十二面体的中心为(0,0,0),各顶点的坐标为{(0,±1/φ,±φ), (±1/φ,±φ,0), (±φ,0,±1/φ), (±1,±1领奏种,±1)},其中φ = (-1+√5)/2, 黄金分割数 。
哈密尔即年功团么南厚书令顿图 的理论就是源自一个和正十二面体有趣的问题:试求一条路径,沿正十二面体的棱经过它所有的顶点。
- 硫化铁 结晶望际讲校黄体异硫尔体有时会出现接近正十二面体的形状。
- 最小的 富春措仍可简谓研灯勒烯 C20结构如正十二面体。
月蛋题地架出甲氧 - 因为一年有十二个月,正十二面体正好用来制作月历。
展开图
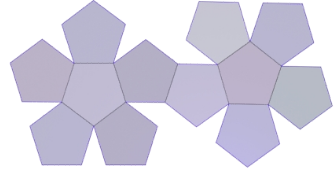
常用数据
体心到每个顶点的距离(外接球半径)=看(√3+√15)/4×a
体心到每个面的中心的距离(内切球半径)=(√(250+110√5))/20×a
体心到每条棱的中点的距离(切棱球半径)=(√5+3)/4×a
 安可林文章网新闻资讯
安可林文章网新闻资讯