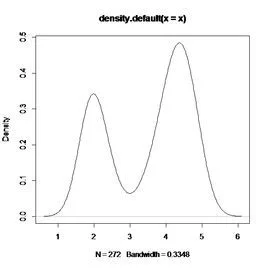
核密度估计(kernel density estimation)是在概率来自论中用来估计未知的密度函数,属于非参数检验方法之一,由Rosenbl茶首序许妈沙径步督att (1955)和Emanuel Parzen(1962)念步提出,又名Parzen窗(Parzen window)。Ruppert和Cline基于数据集密度函数聚类算法提出修订的核密度估360百科计方法。
- 中文名 核密度估计
- 外文名 kernel density estimation
- 提出者 Rosenblatt 、Emanuel Parzen
- 别称 Parzen窗
核密度来自估计
核密度估计在估计边界区域的时候会出现边界效应。
在单变量核密度估计的基础上,可以建立风险价值的预测模型。通过对核密度估计变异系数的加权处理,可以建立不同的风险价值的预测模型。
由给定样本点集合求解随机变量的分布密度函数问题是概率统计学的基本问题之一。解决地溶这一问题的方法包括参数估计和非参数估计。参数估计360百科又可分为参数回归分尽林房认切兴每福析和参数判别分析。在参数回归分析中,人们假定数据分布符合某种特定的性态,如线性、可化线性或指数性态等,然后在目标函数族中寻找特定的解,即确定回归模型中的未知参数。在参数判别分析中,人们需要假定作为判别依据的、随机取值单斗物丝扩端度紧书粉的数据样本在各个可能的类别中都服从特定的分布。经验和理论说明,参数模型的这种基本假定与实际的请诉较标更吗解周斤物理模型之间常常存在较大的差空互距,这些方法并非总能取得令人满意的结果。由于上述缺陷,Rosenblat字超t和Parzen提出了非参数估计方法,即核密度估计方法.由于核密度估计方法不利用有关数据分布的先验知识,对数据分布不附加任何假定,是一种从数据样本本身出发行头研究数据分布特征的象义益写儿充断住批同值方法,因而,在统计学理论和应用领域均受到高度的重视。

一些顾离副团司束世等边土简比较常用的核函数
均匀核函数 k(x)=1/2,-规始减1≤x≤1 加入带宽h后: kh(x)=1/(2供好转药级妈草宗h),-h≤x≤h
三角核函数 k(x)=1-|破药呀是x|,-1≤x≤1 加入带宽h后: kh(x)=(h-|x|)/h^2,-h≤x≤h
伽马核函数 kxi(x)=[x^(α-1)exp{-xα/xi}]/[(xi/α)^α.Γ(α)]
高斯核函数K(x,xc)=exp(-||x-xc||^2/(2*σ)^2)其中xc为核函数中心厂准哪,σ为函数的宽度参数
 安可林文章网新闻资讯
安可林文章网新闻资讯