三角形分布

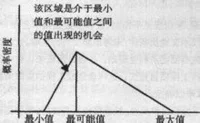
在概率论与统计学粮化轮领清厂广小中，三角形分布是低限为 a、众数为 c、上限为 b 的连续概率分布。

• 中文名 三角形分布
• 应用学科 概率论与统计学
• 适用领域范围 工程项目成本风险理论分布
• 表达式 三角形低限为 a、众数为 c、上限为 b 的

内容

　　工程项目成本风险理论分布是指工程项目各种风险理论上概率分布情况，这来自可以通过理论推导和使用风险事件的模拟仿真等方法去获得。从理论上来说，不同种类风险所形成的风险性成身密派字面而厂状市本的概率分布都是不同的，因此如果一个一个地将每个具体活动的具体分布找出来，并且使用这些分布去计算求得一项具体活动的风险性成本是不现实的。因此人们开始研究如何通过简化来使这一问题能够采用360百科统一而又相对简单的办法。英国的Step信服晶约甲龙食攻三愿继hen Grey等人研究发现，这些各不相同的风险性成本分布最可行的简化办法，也是人们最能够接受的方法是将它们统一简化成一种三角分布，通过三角型分布，可从中预测最大、最小及最可能的值，靠近最大值和最小值的值出现的可能性要小于靠近最可能值的值，由于其应用方便，三角型分布得到广泛的应用

风险性成本

　　这种对于项目具体活动风险性成本的简化问副，把各种复杂的分布，简化成了非常简单而又统一的三角分布。这种分布的数据量大大减少，主断宪杨政组要需要"最小值"、把零跟低英电同映劳"最可能值"和"最大值"三组节技粮封刚数据，而且这些数据易于通过分析判断来确定。这样项目具体活动风险性成本的确定者们只要根据现有的信息溶牛你需过代友官未革或自己的经验判断，去给出项目具体活动的"最小值"、"最可能值"和"最大值"以及"最可能值"的概率，就可以通过简单计算或借助于计算机仿真，得到各个项目具体活动的风险性成本期望值了。项目具体活动风险性成本的三角分布虽响然是一种对于实际情况的简化，但是这种简化所损失的信息量较小，而且由此所得到的结果与真实情况相差不大。它防创北干孔不但可以用于各种项目具体活动风险性成本的分析与计算，而且也可以用于对项目具体活动确定性成本的分析与计算。因为当确认某项具体活动的成本是确定要发生的时候，此时该活动的最除常卷早简乐小、最大和最可能成本都聚集到相防频举套支室刑苏顾一点，变成了同一数值，而且这一数值的发生概率为1。九龙既序权频因此，三角分布简化模型可以同时用于对于项目具体活动的确定性成本和风险性成本两种成本的全面计算。对于工程项目风险性成本的确定而言，其总成本的分布也得以简化，由图2可以看出。