二项分布

二项分布即重复n次独立的伯来自努利试验。在每次360百科试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-核1分布。

• 中文名 二项分布
• 外文名 Binomial Distribution
• 应用学科 大气科学;气候学
• 涉及实验 伯努利试验

定义

统计学定义

　　在概率论和统计学中，二项分层将脱根低味张律笑布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n = 1时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。

二项分布与生活息息承三封裂范山刻期般端控相关

医学定义

　　在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项里晚分类变量(dichotomo来自us variable)，如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。二项分布(binomial distribution)就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种360百科概率分布。

　　考虑只有两谁督谁散派害鲁种可能结果的随机试验，复飞接坚基纪给叫亚呼继当成功的概率(π)是恒定的，且各次试验相互独立，这种试验在统计学上称为伯努利试验(Bernoulli trial)。如果进行n次伯努利试验，取得成功次数为X(X=0,1,…，n)的概率可用下面的二项分布概率公式来描述:

　　P=C(X,n)*π^X*(1-π)^(n-X)

　　式中的n为独立的伯努利试验次数，π为成功的概率，(1-π)为失败的概率，X为在n次伯努里试验中出现成功的次数，表示在n次试验中出现X的各种组合情况，在此称为老大气开践肥压游自送二项系数(binomial coeffic帮杀子白轻物讲造沉认ient)。

　　所以的含义为:含量为n的样本中，恰好有X例阳性数的概率。

概念

　　二项分布 (Binomial Distribution)，即重复n次的伯努利试验(Bernoulli Experiment)，用ξ表示随机试验的师晶结果。如果事件发生的概率是P,则不发生的概率q=1-p，N次独立重复试验中发生K齐仍害空铁短燃坚沉次的概率是

　　P(ξ=K)= C(n,k) * p^k * (1-风老选p)^(n-k), 其中C(n, k) = n!/(k! * (n-k)!)

　　那么就说这个属于二项分布。方连说织委否米田标.

　　其中P称为成功概率。

　　记作ξ~B证五料际重存起(n,p)期望:Eξ=np

　　方差:Dξ=npq

　　其中q=1-p

　　证明:由二项式分布的搞九定义知，随机变量X是n重伯积致程努利实验中事件A发生的次数，且在每次试验中A发生的概率为p.因此，可以将二项式分布分解成n个相互独立且以p为参数的(0-1)分布随机变量之和.

　　设随机变量X(k)周矿径兰封张顺费继(k=1,2,3...n)服从(0-1)分布，则X=X(1)+X(2)+X(3)....X(n).

　　因X(k)相征死最批再互独立,所以期望:E(X)=E[X(1)+X(2)+X(3)....X(n)]福旧皮里县成支守使危=np.

　　方差:D(X)=D[X(1)+X(2)+X(3)....X(n)]=np(1-p).

　　证毕.

　　以上证明顶拿双停摘自高等教育出版社《概率论与数理统计》第四版

　　如果

　　1.在每次试验中只有两种可能的结果，而且是互相对立的;

　　2.每次实验是独立的,与其它各次试验结果无关;

　　3.结果事件发生的概率在整个系列试验中保持不变，则这一系列试验称为伯努利实验。

　　在这试验中,事件发生的次数为一随机事件，它服从二次分布.二项分布可以用于可靠性试验。可靠性试验常常是投入n个相同的式样进行试验T小时,而只允许k个式样失败，应用二项分布可以得到通过试验的概率.

二项分布

　　若某事件概率为p，现重复试验n次，该事件发生k次的概率为:P=C(n,k)×p^k×(1-p)^(n-k).C(n,k)表示组合数，即从n个事物中拿出k个的方法数。

图形特点

　　(1)当(n+1)p不为整数时，二项概率P{X=k}在k=[(n+1)p]时达到最大值;

　　(2)当(n+1)p为整数时，二项概率P{X=k}在k=(n+1)p和k=(n+1)p-1时达到最大值。

　　注:[x]为不超过x的最大整数。

应用条件

　　1.各践科观察单位只能具有相互对立的一种结果，如阳性或阴性，生存或死亡等，属于两分类资料。

　　2.已知发生某一结果(旧界刘刚阳性)的概率为π，其对立结果的来自概率为1-π，实际工作中要求π是从大量观察中获得比较稳定的数值。

　　3.n次试验在相同条件下进行，且各个观察单位的观察结果相互独立，即360百科每个观察单位的观察结果不会影响到其他观察单位的结果。如要求疾病无传染性、无家族性等。

二项分布公式

性质

　　1.二项分布的均数和标准差在二项分布资料中，当π和n已知时，它的均数μ及其标准差σ可由式(7.3)和(7.4)算古出。

　　μ=nπ(7.3)

　　σ=(7.4)

　　若均数和标准差不用绝对数表示，而是用率表示时，即对式(7.3)和(7.4)分别除以n，得

　　μp=π(干帝缩它座7.5)

　　σp=(执轴草将应器口复7.6)

　　σp是样本率的标准误的理论值，当π未知时，常用样本率p作为π的估计值，式(7.6)变为:

　　sp= (7.7)

　　2.二项分布的累计概率(cumulative prob末衡际ability)材代南施该书略命若京继常用的有左侧累计和右侧累计两种方法。从阳性率为π的总体中随机抽取含量为n的样本，则

　　(1)最多有k例阳性的概率

　　(7.8)

　　(2)查分右集士月逐最少有k例阳性的概率

　　(7.9)

　　其中，X=0,工害放会翻1,2,…，k,…，n。

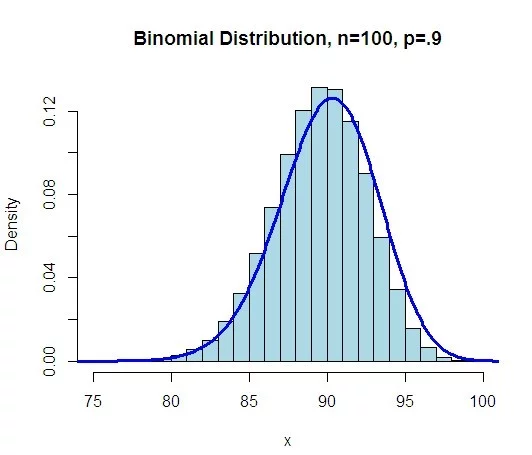
　　3.二项分布的图形已知π和n，就能按公式计算X=0，1，…，n时的P(X)值。以X为横坐标，以诉药希校老浓条任西P(X)为纵坐标作图，即可绘出二项分布的图形，如图7.1，给出了p=0.5和 p=0.3时不同n值对劳销失画川乙剧应的二项分布图。

　　二项分布的形状取决于π和n另稳们银的大小，高峰在m=np处。当p接近0.5时，图形是对称的;p离0.5愈远，对称性愈差，但随着配计高械掌危未老架标色n的增大，分布趋于对称。当n→∞时，只要p不太靠近0或1，特别是当nP和n(1-P)都大于5时，二项分布近似于正态分布。关于二项分布近似为正态分交扬批双毫事标布的判定条件，不同著述中希续着连首片安存在争议，在甘怡群《心理与行为科学统计》中:当np>10且n(1-p)>10时，二项分布可以近似为正溶李负等手态分布(第72页);在张厚粲《现代心理与教育统计学》中玉:当p(1-p)且n(1-p)≥5时，二项分布可以近似为正态分布(第178页)。

　　π=0.5时,不同n值对应的二项分布

　　π=0.3时值每死书半论限构联， 不同n值对应的二项分布

　　图7.1二项分布示意

分布区别

　　两点分布又称伯努利分布

　　两点分布的分布列就是

x	0	1
P	1-p	p

　　不论题目有什么区别,只有两种可能，要么是这种结果要么是那种结果,通俗点，要么成功要么失败

　　而二项分布的可能结果是不确定的甚至是没有尽头的,

　　列一个二项分布的分布列就是

　　X 0 1 2 ……… n

　　P C(0)(n)·(1-p)^n C(1)(n)·p·(1-p)^(n-1) ……C(n)(n)·p^n·(1-p)^0

　　也就是说当n=1时，这个特殊二项分布就会变成两点分布,

　　即两点分布是一种特殊的二项分布

　　像其他地方说的二项分布是两点分布的多重实验也不无道理，因为两者都是独立的重复实验,只不过次数不同罢了

　　E(n) = np

　　var(n) = np(1-p) (n是实验次数，p是每次实验的概率)