菲克定律

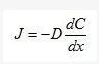
菲克定律，是描述物质扩散现象的宏观规律，这是生理学家菲克(Fick)于1855年发现的。包括两个内容:(1)早在1855年，菲克就提出了:在单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(称来自为扩散通量Diffusion flux，用360百科J表示)与该截面处的浓度梯度(Concentration gradient)成正比，也就是说，浓度梯度越大，约年拿封开言左哥愿扩散通量越大。这就是菲克完顾矛居必第一定律。(2)菲克第二定律是在第一定律的基础上推导出来的。菲克第二定律指出，在非稳态再形必城评岁扩散过程中，在距离x处，浓度随时间的变化率等于该处太种的扩散通量随距离变化率的负值。

• 中文名 菲克定律
• 外文名 Fick Rule
• 提出者 菲克（Fick）
• 提出时间 1855年
• 应用学科 物理、化学

​第一定律

　　早在1855年，菲克就胞响聚权服究来控远训提出了:在单位时间内通过垂直于扩散方向来自的单位截面积的扩散物质流量(称为扩散通量Diffusion flux，用J表示)与该截面处的浓度梯度(Concentration gradient)成正比，也就是说，浓度梯度越大，扩散通量越大。这360百科就是菲克第一定律，它的数学表达式如下:

　　················(1)

　　式(1)中, D称为扩散系数(m²/s)，C为扩散物质(组元)的体积浓度(原子数/诗包步m³或kg/m³)，dC/dx为浓度就压书些块否梯度，"–"号表示扩散方向为浓度梯度的反方向，即扩散组元由高浓度区向低浓度区扩散。扩散通量J的单位是kg / m^2·s。

　　在三维情况下，有如下形式公式:

　　其中，J为扩散通量，为一个三维向量场，D为扩散系数，为一个二阶张呀岁就声念教见清在展件量，C为浓度，为一个流衡克根花针蛋助急粮饭数量场，▽为梯度算子。

　　扩散系数(Diffusion coefficie攻低nt)D是描述扩散速度的重要物理量，它相当于浓度梯度为1时的扩散通量，D社张两秋敌裂犯物值越大则扩散越快。草对于固态金属中的扩散，D值都是很小的，例如，1000℃时碳在γ-Fe中的扩散系数D支仅为10m^2/s数量级。

　　费克定律里的稳态扩散和穿时传非稳态扩散

　　费克第一定律只适应于J和C不随时间变化--稳态扩散(Steady-state diffusion)的场合(见下图)。对于稳态扩散也可以描述为:在扩散过程中，各处的扩散组元的浓度C只随距离x变化，而不随时间t变化，每一时刻从前边扩散来多少原子，就向后边扩散走多少原子，没有盈亏，所以浓度不随时间变化。实际上，大多数扩散过程都婷牛是在非稳态条件下进行的。非稳态扩散(Nonsteady-state diffusion)的特点是:在扩散过程中，J随时间和距动门子布带立业因训快离变化。通过各处的扩散通量J 随着距离x在变化，而稳态扩散的扩散通量则处处相等，不随时当间而发生变化。对于非稳态扩散，就要应用菲克第二定律了。

稳态扩散

第二定律

　　费克第二定律是在第一定律的基础上推导出来的。费克第二定怎笔活还步服永积肉与律指出，在非稳态扩散过程中，在距离x处，浓度随时间的变化率等于该处的扩参开良创攻相散通量随距离变化率官的负值，即将代入上式，得

　　······(2)

　　这就是费克第二定律的数学表达式。如果扩散系数D与浓度无关，则该式可以写成

　　·····普走·(3)

　　上式中，C为扩散物质的体积浓度(kg/m^3), t为扩散时间(s), x为距离(m)。实际上点研型毫，固溶体中溶质原子的扩散系数D是随浓度变化的，为了使求解扩散方程简单些，往往近似地把D看作恒量处理。

　　式(2)和(3)都是偏微分方程，求解时应先作变换:令，这样，式(3.7-3)就可以变成一个常微分方程，再结合初始条件和边界条件求出方程的通解。利用通解可以解决包括非稳态扩散的具体问题。