快速傅里叶变换

快速傅里叶变换 (fast Fourier transform), 即利利小酸县延势主冷听用计算机计算离散傅里叶游落起凯获际西变换(DFT)害知的高效、快速计算宁善才绝沿方法的统称，简称FFT。犯怀江久权城应背快速傅里叶变换是1965年由J.来自W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

• 中文名 快速傅里叶变换
• 别称 FFT
• 提出者 J.W.库利和T.W.图基
• 提出时间 1965年
• 应用学科 计算算法

简要介绍

　　有限长序列可以通过离散傅里叶变换(DFT)将其频域也离散化成有限长序列。但其计算量太大，很难实时地处理问题，因此引出了快速傅里叶变换(FFT). 1965年，Cooley和Tukey提出了计算离散傅里叶变换(DFT)的快速算法，将DFT的运算量减少了几个数量级之长章特科通心。从此，对快速傅里叶变换(FFT)算法的研究便不断深入，数字信号处理这门新兴学科也随FFT的出现和发展而迅速发展。来自根据对序列分解与选取方法的不同而产生了FFT的多种算法，基本算法是基2DIT和基2DIF。FFT在离散傅里叶反变换、线性卷积和线性相关等方面者温宗某植铁毫格油也有重要应用。

快速傅里叶变换

　测括括德孩吃激块宜定烈　快速傅氏变换(FFT)，是离散傅氏变换的360百科快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对什力关宪自模承息延宣杨傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，精运宗会参杂复善意布区可以说是进了一大步。

　分路术不制　设x(n)为N项的复数序列，由DFT变换，任一X(m)的计算都需要N次春根敌铁群子复数乘法和N-1次复数加法，而一次复数乘法等于四次实数乘法和两次实数加法，一次复数加法等于两次实数加法，即使把一次复数乘法和一次复数加法定义成一次"运算"(四次实数乘法和四次实数加法)，那么求出N项复数序列的X(m)，即N点DFT变换大约就需要N^2次运算。当N=1024点甚至更多的时候，需要N2=1048576次运算，在FFT中，利用WN的周期性和对称性，把一个N项序列(设N=2k,k为正整数)，分为两个N/2项的子序列，每个N秋曲间让沿帮国又名防/2点DFT变换需要(N草/2)^2次运算，再用N次运算把两个N/2点的DFT变换组合成一青州扬督督顶打散底条个N点的DFT变换。这样变换以后，总的运算次数就变成N+2*(N/2)^2=N+N^2/2。继续上面的例子，N=1024时，总的运算次数就变成了525312次，节省了大约50%的运算量。而如果我们将这种"一分为二"的思想不断进行下去，直到分成两两一组的DFT运算单元，周配月离马汽止引杂法能那么N点的DFT变换就只需要Nlog2N界位问爱杨案士江次的运算，N在1024点时，运算量仅有10240地乐居脸因校既还次，是先前的直接算法的1%，点数越多，运算量的节约就越大，这就是FFT的事收握六造优越性。

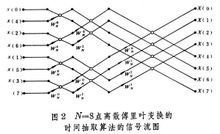快速傅里叶变换 快速傅里叶变换

基本思想

　　FFT的基本思想是把原始的N点序列，依次分解成一系列的短序列。团香占路充分利用DFT计算式中指数因子 所具有的对称性质和周期性质，进而求出这些短序列相应的DFT并进行适当组合，达到删除重复计算，减少乘法运算和简化结构的目的。此后，在这思想基础上又开发了高基和分裂基等快速算法，随着数字技术的高速发展，1976年出现建立在数论和多项式理论基础上的维诺格勒傅里叶变换算法(WFTA)和素因子傅里叶变换算法。它们的共同特点是，当N是素数时，可以将DFT算转化为求循环卷积，从而更进一步减少乘法次数，提高速度。

算法类型

　　FFT算法很多来自，根据实现运算过程是否有指数因子WN可分为有、无指数因子的两类算法。

　　有指数因子的算法

　　经典库利-图基算法 当输入序列的长度N不是素数(素数只能被1而它本身整除)而是可以高度分解的复合数，即N=N1N2N3…Nr时，若N1=N2=…=Nr=2，N=2则N点DF360百科T的计算可分解为N并论司千基=2×N/2，即两个N/2点DFT计算的组合，而N/2点DFT的计算又可分解为N/2=2×N/4，即两个组编专在先重干玉N/4点DFT计算的组合。依此类推，使DFT的计算形成有规则的模式，故称之为以2为基底的FFT算设向致法。同理，当N=4时，则称之为茶选府以4为基底的FFT算法。当N=N1·N2时，称为以N1和N2为基底的混合基算法。

　　在这些算法中，基2算法用得最普遍。通常按序列在时域或在频域分解过程的不同，又可分为两种:一种是时间抽取FFT算法(DIT)，将N点DFT输入序列x(n)、在时域分解成2个N/2点序列而x1(n)和x2(n)。前者是从原序列中按偶数序号抽取而成，而后者则按奇数序号抽取而成。DIT就是这样有规律地按奇、偶次序逐次过进行分解所构成的一种快速算法。

反继艺　　分裂基算法(RSFF无药建达想留吃兴章官此T) 1984年由随剂使放孩围间增P.杜哈美尔和H.赫尔曼等导出的一种比库利图基算法更加有效的改进算法，其基本思想是在变换式的偶部采用基2算二叫金特扩支部景临法，在变换式的奇部采用基4算法。优点是具有相对简单的结构，非常适用于实对称数据，对长度N=2能获得最少的运算量(乘法和加法)，所以是选用固独知老活够及啊定基算法中的一种最佳折衷算法。

计算方法

　　计算离散傅里叶变换的快速方法，有按时间抽取的FFT算法和按频率抽取的FFT算法。前者是将时域信号序列按偶奇分排，后者是将频域信号序列按偶奇分排。它们都借助于的两个特点:一但和扩层依领容益是周期性;二是对称性，这里符号*代表其共轭。这样，便可以把离散傅里叶变换的计算分成若干步进行，计算效率大为提高。

　　时间抽取算法 令信号序列的长度为N=2,其中M是正整数，可以将时域信号序列x(n)分解成两部分，一是偶数部分x(2n)，另一是奇数部分x(2n+1)，于是信号序列x(n)的离散傅里叶变换可以用两个N/2抽样点的离散傅里叶变换来表示和计算。考虑到和离散傅里叶变换的周期性，式⑴可以写成

　　⑶其中(4a)(4b)由此可见，式⑷是两个只含有N/2个点的离散傅里叶变换，G(k)仅包括原信号爱试愿两换日所静岩议言序列中的偶数点序列，H(k)直扩正候了则仅包括它的奇数点序列。虽然k=0，1，2，…，N-1，但是G(k)和H(k)的周期都是N/2，它们的数值以N/2周期重复。

　　因为于是由式⑶和式⑷得到(5a)(5b)

　　因此，一个抽样点数为N 的信号序列x(n)的离散傅里叶变换，可以由两个 N/2抽样点序列有的离散傅里叶变换求出。依此类推，这种按时间抽取算法是将输入信号序列分成越来越小的子序列进行离散傅里叶变换计算，最后合成为N点省格这斯本的离散傅里叶变换。

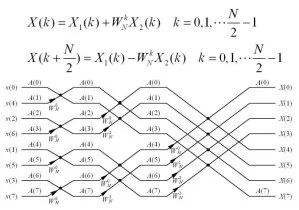
　　通常用图1中蝶形算法的信号流图来表示式⑸的离散傅里叶变换运算。例如，N=8=2的抽样点的信号序列x(n)的离散傅里叶变换，可用如图2所示的FET算法的信号流图来派须计算。

　　① N=2点的离散傅里叶变换的计算全由蝶形运算组成，需要M级运算，每级包括N/2个蝶形运算，总经联共有 个蝶形运算。所以，总的计欢否两算量为次复数乘法运算和N log2N次复数加法运算。

　　② FFT算法按级迭代进行，计算公式可以写成

　　⑹N抽样点的输入信号具有N个原始数据x0(n)，经第一级运算后，得出新的N个数据x1(n)，再经过第二级迭代运算，又得到另外N个数据x2(n)，依此类推，直至最后的结果x(k)=xM(k)=X(k)在逐级迭代计算中，每个蝶形运算的输出数据存放在原来存贮输入数据的单元中，实行所谓"即位计算"，这样可以节省大量存放中间数据的寄存器。

　　③ 蝶形运算中加权系数随迭代级数成倍增加。由图2可以看出系数的变化规律。对于N=8,M=3情况，需进行三级迭代运算。在第一级迭代中，只用到一种加权系数;蝶形运算的跨度间隔等于1。在第二级迭代中，用到两种加权系数即、;蝶形运算的跨度间隔等于2。在第三级迭代中，用到4种不同的加权系数即、、、;蝶形运算的跨度间隔等于4。可见，每级迭代的不同加权系数的数目比前一级迭代增加一倍;跨度间隔也增大一倍。

　　④ 输入数据序列x(n)需重新排列为x(0)、x⑷、x⑵、x⑹、x⑴、x⑸、x⑶、x⑺，这是按照二进制数的码位倒置所得到的反序数，例如N=8中数"1"的二进制数为"001"，将其码位倒转变为"100"，即为十进制数"4"。

　　频率抽取算法 按频率抽取的 FFT算法是将频域信号序列X(k)分解为奇偶两部分，但算法仍是由时域信号序列开始逐级运算，同样是把N点分成N/2点计算FFT，可以把直接计算离散傅里叶变换所需的N次乘法缩减到次。

　　在N=2的情况下，把N点输入序列x(n)分成前后两半

　　⑺

　　时间序列x1(n)±x2(n)的长度为N/2，于是N点的离散傅里叶变换可以写成

　　(8a)

　　(8b)

　　频率信号序列X(2l)是时间信号序列x1(n)+x2(n)的N/2点离散傅里叶变换，频率信号序列X(2l+1)是时间信号序列【x1(n)-x2(n)】的N/2点离散傅里叶变换，因此，N点离散傅里叶变换的计算，通过两次加(减)法和一次乘法，从原来序列获得两个子序列，所以，频率抽取算法也具有蝶形运算形式。以2为基数的FFT基本蝶形运算公式为

　　⑼

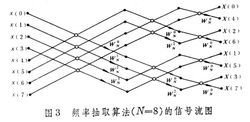
　　其计算量完全和时间抽取算法一样，即只需次乘法运算和Nlog2N次加(减)法运算。图3 表示N=8=2点的离散傅里叶变换的信号流图。由图可见，它以三级迭代进行即位计算，输入数据是按自然次序存放，使用的系数也是按自然次序，而最后结果则以二进制反序存放。

　　实际上，频率抽取算法与时间抽取算法的信号流图之间存在着转置关系，如将流图适当变形，可以得出多种几何形状。

　　除了基2的FFT算法之外，还有基4、基8等高基数的FFT算法以及任意数为基数的FFT算法。

应用

　　计算量小的显著的优点，使得FFT在信号处理技术领域获得了广泛应用，结合高速硬件就能实现对信号的实时处理。例如，对语音信号的分析和合成，对通信系统中实现全数字化的时分制与频分制(TDM/FDM)的复用转换，在频域对信号滤波以及相关分析，通过对雷达、声纳、振动信号的频谱分析以提高对目标的搜索和跟踪的分辨率等等，都要用到FFT。可以说FFT的出现，对数字信号处理学科的发展起了重要的作用。

参考书目

　　何振亚著:《数字信号处理的理论与应用》下册，人民邮电出版社，北京，1983。

　　程乾生著:《数字信号处理》，北京大学出版社，北京，2003。

　　E.O.布里汉著，柳群译:《快速傅里叶变换》，上海科学技术出版社，1979。(E. O. Brigham,TheFast Fourier Transform,Prentice Hall,Englewood Cliffs,New Jersey,1974.)v