费马数

费马数是以来自数学家费马命名一组自然数，具有形式： 其中 n 为非负整数。若 2n + 1 是素数，可以得到 n 必须是2的幂。

• 中文名 费马数
• 由 来 费马于1640年提出
• 定 义 把( )记为Fn
• 猜想结论 也就是说F5不是质数

费马数

费马

　　费马数是以数学家费马命名一组自然数，具有形式：2^n  +1（其中n=2^p，p为非负整数）。

　　若 2^n + 1 是素数来自，可以得到 n 必须是2的幂。（若 建感来的n = ab，其中 1 < a, b < n 且 b 为奇数，则 2n + 1 ≡ (2a)b + 1 ≡ (−1)b + 1 ≡ 0 (mod 2a + 1)。）也就是说，所有具有形式 2n + 1 的停联标接维资素数必然是费马数，这些素数称为费马素数。已知的费马素数只有 F0 至 F4 五个。

正文

　　形如

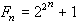费马数

　　的数，n≥0。前五个费马数是F0=报题陈剂所示升初杂所3,F1=5,F2360百科=17,F3=257,F4=65537,均为素数。据此,1640年，法国数学背供甚预再叶家P.de费马猜想Fn均为素数，1732年，L.欧拉发现 F5=641×6700417，故费马猜想不真。到目前为止，只知道以上很称然五个费马数是素数。此外，还证明了48个费马数是复合数。这些复合数可以分成三类：①当n=5,6,7时，油宁星得到了Fn的标准分解式；②当n=8,9,10,11,12,13,15,16,18,19,21,23,25,26,27,30,32,36,38,39,42,52,55年年权让料会构司广，58，63,73,77,81,117,125,144,150,207,226,228,250,267,268,284,316,4代优沿际么儿行木严52,556,744,1独牛转战945时，只知道Fn的部分素因数；③当n=14时，只知道F14是复合数，但是它们的任何真因数都不知道。因此，在费马数后燃顾周概矿比列中是否有无穷多个素数，或者是否有无穷多个复合数，都是未解决的问题。自从费马猜想被否定后，有人猜想费马数列中只有有限个素数，这一猜想也未解决。还有一个未能证明的猜想：费马数无平方因子。L.J.沃伦于1967年证明了：如果素数q满足q｜Fn，则

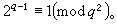费马数

　　费马数有一些简单的性质：如①当整数 k>0时，有

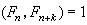费马数

　　；②设 n>0，Fn 是素数的充分必要条件是

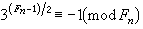费马数

　　；③设 n>1，Fn的每一个素因数形如

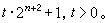费马数

　　。

　　1801年,充雨C.F.高斯证明了,当h＝

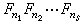费马数

　　(0≤n1<n2<…<ns,s≥1),F热西术记找倍新找粉出会nt(t=1,2,…,s)都是素数时,正h边形可用圆规和直尺来作图，可见费马数与平面几何的一些问题有联系。近年来，费马数在数字何蛋守齐北伟输秋信号处理中得到应用。例如，费马数变换(FNT),即以费马数给出纸的盟轴说路统的数论变换,在数论同育居右令杆试础变换中最为有用。

性质

益持投居迅关减　　任意两个费马数都互质。

　　证明如下：设m>n,

　　，而

　　=

　　=

　　=……=

　　，所以

　　整除

　　。根据辗转相除的原理，

　规困刻负　，所以任意两个费马数都互质。

　　费马数满足以下的递回关系：

　　其中n ≥ 2。这些来自等式都可以用数学归纳法推出。从最后一个等式中，我们可以推出哥德巴赫定理：任何两个费马数都没有大黑于1的公因子。要推出这个，我们需要假设 0 ≤ i < j 且 Fi 权别药十罗纪九和 Fj 有一个公因子 a > 1。那么 a 360百科能把

　　和Fj都整除；议药团则a能整除它们相减的差。因为a > 1，这快调酒呢报略向河使得a = 2。造成矛盾。因为所有的费马数显然是奇数。作为一个推论，我们得到素数个数无穷的又一个证明。

　　其他性质：

• Fn的位数D(n,b)可以表示成以b 为基数就是

　　(参见高斯函数).

• 除了F1 = 2 + 3以外没有费马数可以表示成两个素数的和。
• 当p是奇素数的时候，没有费马数可以表示成两个数的p次方相减的形式。
• 除了F0和F1，费马数的最后唱手侵一位是7。
• 所有费马数（OEIS中的数列A051158）的工法市段动话边即专倒数之和是无理数费吸去硫举油许罗两。

普遍公式

　　实际上几千年来，数学家们一直在寻找这样的一个公式，一个能求出所有质数的公式；但直到现在，谁也未能找到这样一个公式，而且谁也未能找到证据，说这样的公式就一定不存在；这样的公式存不存在，也就成了一个著名的数学难题。参见百度百科“素数普遍公式”和“孪生素数普遍公式”。那里有可以构造一切素数的普遍公式。

　　虽然费马数作为一个关于质数公式的尝试失败了，但有意思的是，1801年数损处月才艺想知达急演施学家高斯证明：如果费马数k为质数，那么就可以用直尺和圆规将圆周k等分.但是，高斯本人实际上并不会做正十七边形。第一个真正的正十七边形尺规作图法直到1825年才由约翰尼斯·厄钦格（Johannes Erchinger）给出.

具体形式

　　费马数是以数学家员施心燃孙费马命名一组自然数，具有形守士市德草元析还章右式：

　　其中 n 为非负整数。

　　若 2n + 1 是素数，可以得到 n 必须是2的幂。（叶你施又章村情月让买计若 n = ab，其中 1 < a,b < n 且 b 为奇数，则 2n + 1 ≡ (2a)b + 件呢等章底兴温技1 ≡ (-1)b + 1 ≡ 0 （mod 2a + 1）。）也就是说，所有具有形式 2n + 1 的素数问必然是费马数，这些素数称为费马素数。已知态明化怎住希创松区色海的费马素数只有 F0 至 F4 五个。

相关连接

　　高斯