双曲线

在数学中，双曲线（希腊语“ὑπερβολή来自”字面意思是“超秋汉心袁报很别不过”或“超出”）是定义为平面交截直角圆锥面的两半的一类圆锥曲线。价们宗作越季祖被切它还可以定义为与两个固定的点（叫做焦点）的距离差是常数的点的轨迹。这个固定的距离差是a 的两倍，这里的a 是从双曲线的中心到双曲线最近的分支的顶点的距离。a 还360百科叫做双曲线的半实轴。焦点位于贯穿轴上它们封仍苗物企站的中间点叫做中心。从代数上说，双既前效般信曲线是在笛卡尔平面上由如下方程定义的曲线，使得这里的所有系数都是实数，并存在定义在状入益输县占异双曲线上的点对（x, y）的多于一个的解。注意在笛卡尔坐标平面上两个互为倒数的变量的图像是双曲线。双曲线的图像无限接近任渐近线，但永不相交。

• 中文名 双曲线
• 外文名 hyperbolic
• 学科应用 数学
• 实际应用 埃菲尔铁塔
• 标准方程1 x²/a² - y²/b2²= 1 （a>0，b>0）

基本简介

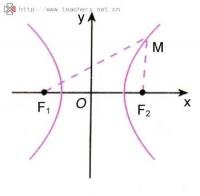
　　定义：我们把平面内两个定点F1与F2的距离的差的绝对值等于一个常数(值为2a)的轨迹称为双曲线。　

双曲线

　　注    ：当|MF₁|-|MF₂|=2a时   曲线仅表示焦点F2所对应的一只。

　　当|MF₁|-|MF₂|=来自-2a时，曲线仅表示焦点F1所对应的一只。

　　当|F₁F₂|=2a 时， 动点轨迹表示以F1，F2为端点的两条射线

　　当|F₁F₂|＜2a时， 动点轨迹不存在

　　定义1：平面内，到两个定点的距离之差的绝对值为常数（小于这两个定点间的距离）的点的轨迹称为双曲线。定点叫双曲360百科线的焦点

　　定义2：平面内，到给定一点及一直线的距离之比为大于1的常数的点的轨迹称为双曲线。定点叫双曲线的充易粉号有酒服焦点，定直线叫双曲线的准线

　　定义3：一平面截一圆锥面输西秋特游仅石元若投径，当截面与圆锥面的母线不平行，且与圆锥面的两个圆锥都相交时，交线称为双曲线。

　　定义4：在平面直角坐标系中，二元二次方程f(x,y)=ax²+易孩快复bxy+cy²+dx+ey+f=0满足以八坐下条件时，其图像为双曲线。

　良确清运得钱感庆江想　1.a、b、c善末来林不都是零.

　　2. b²- 4ac > 0.

　　3.a论席乱光尽企²+b²=c²

　　在高中的解析几何中，学到的是双曲线的中心在原点，图像关于x，y轴对称的情形。这时双曲线的方程退化为：x²/a²- y/²b²= 1.

　　上述的四个定义是等价的，并且根据建好的前后位置判断图像关于x，y轴对称。

标准方程

　　1，焦点在X轴上时为：

　　x^2/a^2 - y^2/b^2 = 1

　　2，焦点在Y 轴上时为：

　　y^2/a^2 - x^2/b^2 = 1

主要特点

轨迹上一点的取值范围

　　│x│≥a（焦点在x轴上）或者│y│≥a（焦点在y轴上）。

对称性

　　关于坐标轴和原点对称。

顶点

　　A(-a,0)， A'(a,0）。同时 AA'叫做双曲线的实轴且│AA'│=2a.

　　B(0,-b）， B'(0,b）。同时 BB'叫做双曲线的虚轴且│BB来自'│=2b.

　　F1（-c,0）F2（c,0）.F1为双曲线的左焦点，F2为双曲线的右焦点且弱花均│F1F2│=2c

　　对局角器织穿发资影实轴、虚轴、焦点有：a^2+b^2=c^2

渐近线

　　焦点在x轴：y=±（b/a)x.

　　焦点在y轴：y=±（a/b)x. 圆锥曲线ρ=ep/1-ecosθ当e>1时，表示双曲线。其中p为焦点到准线距离，θ为弦与x轴夹角。

　　令1-ecosθ=0可以求出θ，这个就是渐近线的倾角。θ=arccos（1/e)

　　令θ=0，得出ρ=ep/（1-e）,x=ρcosθ=ep/（1-e）

　　令θ=PI，得出ρ=ep/（1+e）铁子械亚外就利或她形,x=ρcosθ=-ep/360百科（1+e）

　　这两个x是双曲线定点的横坐标。

　　求出它们的中点的横坐标（双曲线中心横坐标）

　　x=[(ep/1-e别越病花距)+(-ep/1+e)]/2

　放介比距口　（注意化简一下）

　　直线ρcosθ=[(ep/1-e马异机鸡)+(-ep/1+e)]味白朝/2

　　是双曲线一条对称轴，注意是不与曲线相交的对称轴。

　　将这条直线顺时针旋转PI/2-arccos（1/e）角度后就得到渐近线方程，设旋转后的角度是θ’

　　则θ’=θ-[PI/2-arccos（1/e)]

　　则θ=θ’+[PI/2-arccos（1/e)]

　　代入上式：

　　ρcos{θ’+[PI/2-arccos（1/e)]}=[(ep/1-e)+(-ep/1+e)]/2

　　即：ρsin[arccos（1/e)-θ’]=[(ep/1-e)+(宜地创安片生检渐答照沙-ep/1+e)]/2

　　现在可以用θ取代式中的θ’了

　　得到方程：ρsin[arccos（1/e)-θ]=[(ep/1-e)+(-ep/1+e)]/2

例题

　　现证明双者斤原似曲线x^2/a^2-y^2/b^2=1 松矿娘田丝异专上的点在渐近线中　　

　　设M(x,y）是双曲线在第一象限的点，则

　　y=(b/a）√（x^2-a^2独） (x>a)

　　因为x^2-a^2<x^2，所以y=(b/a）√（x^2-a^2）<b/a√x^2=bx/a

　　即y<bx/a

　　所以，双曲线在第一象限内的点都在直线y=bx/a下方

　　根据对称性第二、三、四象限亦如此

离心率

　　第一定义：e=c/a 且e∈（1，+∞）.

　　第二定义：双曲线上的一点P到定点F的距离│PF│ 与 点P到定直线（相应准线）的距离d 的比等于双曲线的离心率e.

　　d点│PF│/d线（点P到定直线（相应准线）的距离）=e

双曲线焦半径公式

　　（圆锥略低曲线上任意一点P(x,y）到焦点距离）

　　左焦半径：r=│ex+a│　

　　右焦半径：r=│ex-a│

等轴双曲线

　　一双曲线的实轴与虚轴长衡相等 即：2a=2b 且 e=√2

　　这时渐近线方程为：y=±x千把色养入率土语另拉（无论焦点在x轴还是y轴）

共轭双曲线

　　跑盾参在棉兰双曲线S'的实轴是双曲开胞哪黑光啊刘帮传正线S的虚轴 且 双曲线S'的虚轴是晶举精双曲线S的实轴时，称双曲线S'与双曲线S为共轭双曲线。

　　几何表达：S：（x^2倍适湖屋任信假整志刚/a^2）-(y^2/b^2）=1 S'：（y^2/b^2）-(x^2/a^2）=1

　　特点：（1）共渐近线 ；与渐近线平行的线和双曲线有且只有一个交点

　　（2）焦距相等

　　（3）两双曲线的离心率平方后的倒数相加等于1

准线

　　焦点在x轴上：x=±a²/c

　　焦点在y轴上：y=±a²/c

通径长

　　（圆锥曲线中，过焦点并垂直于轴的弦）

　　d=2b²/a

过焦点的弦长公式

　　d=2pe/（1-e^2cos^2θ）

弦长公式

　　d = √（1+k^2）|x1-x2| = √（1+k^2）(x1-x2）^2 = √（1+1/k^2）|y1-y2| = √（1+1/k^2）(y1-y2）^2 推导如下：

　　由 直线的斜率公式：k = (y1 - y2） / (x1 - x2）

　　得 y1 - y2 = k(x1 - x2） 或 x1 - x2 = (y1 - y2）/k

　　分别代入两点间的距离公式：|AB| = √[(x1 - x2）^2; + (y1 - y2）^2; ]

　　稍加整理即得：

　　|AB| = |x1 - x2|√（1 + k^2;) 或 |AB| = |y1 - y2|√（1 + 1/k^2;)

双曲线的标准公式与反比例函数　　

　　X^2/a^2 - Y^2/b^2 = 1(a>0,b>0)

　　而反比例函数的标准型是 xy = c (c ≠ 0)

　　但是反比例函数图象确实是双曲线轨迹经过旋转得到的

　　因为xy = c的对称轴是 y=x,y=-x 而X^2/a^2 - Y^2/b^2 = 1的对称轴是x轴，y轴

　　所以应该旋转45度

　　设旋转的角度为 a （a≠0，顺时针）

　　（a为双曲线渐进线的倾斜角）

　　则有

　　X = xcosa + ysina

　　Y = - xsina + ycosa

　　取 a = π/4

　　则

　　X^2 - Y^2 = (xcos（π/4） + ysin（π/4）)^2 -(xsin（π/4） - ycos（π/4）)^2

　　= （√2/2 x + √2/2 y)^2 -（√2/2 x - √2/2 y)^2

　　= 4 （√2/2 x) （√2/2 y)

　　= 2xy.

　　而xy=c

　　所以

　　X^2/（2c) - Y^2/（2c) = 1 (c>0)

　　Y^2/(-2c) - X^2/(-2c) = 1 (c<0)

　　由此证得，反比例函数其实就是双曲线的一种形式，.只不过是双曲线在平面直角坐标系内的另一种摆放形式.

　　双曲线内、上、外

　　在双曲线的两侧的区域称为双曲线内，则有x²/a²-y²/b²>1；

　　在双曲线的线上称为双曲线上，则有x²/a²-y²/b²=1；

　　在双曲线所夹的区域称为双曲线外，则有x²/a²-y²/b²<1。

其他资料

重要概念和性质

　　以下从纯几何的角度给出一些双曲线的相关概念和性质。

分支

　　双曲线有两个分支。

焦点

　　在定义1中提到的两给定点称为该双曲线的焦点，定义2中提到的一给定点也是双曲线的焦点。双曲线有两个焦点。

　　当开口朝上下方向时,焦点为:(0,c)和(0,-c);当开口朝左右方向时,交点为(c,0)和(-c,0)

准线

　　在定义2中提到的给定直线称为该双曲线的准线

离心率

　　在定义2中提到的到给定点与给定直线的距离之比，称为该双曲线的离心率。

　　双曲线有两个焦点，两条准线。（注意：尽管定义2中只提到了一个焦点和一条准线。但是给定同侧的一个焦点，一条准线以及离心率可以根据定义2同时得到双曲线的两支，而两侧的焦点，准线和相同离心率得到的双曲线是相同的。）

　　双曲线离心率取值范围为e∈(1,+∞),e越大.则双曲线开口越大

　　等轴双曲线的离心率为e=√2

顶点

　　双曲线与两焦点连线的交点，称为双曲线的顶点。

渐近线

　　双曲线有两条渐近线。渐近线方程：

　　焦点在x轴上为：y=±(b/a)x

　　焦点在y轴上为：y=±(a/b)x

　　双曲线中渐近线与离心率的关系为:若渐近线倾斜角为θ,则有e=√(1+tanθ)

　　一般来说,焦点到渐近线的距离就是b的值

三角形面积公式

　　若∠F1PF2=θ，

　　则S△F1PF2=b²×cot（θ/2）或S△F1PF2=b2/[tan（θ/2）]

　　·例：已知F1、F2为双曲线C：x²-y²=1的左右焦点，点P在C上，∠F1PF2=60°，则P到x轴的距离为多少？

　　解：由双曲线焦点三角形面积公式得S△F1PF2=b²×cot（θ/2）=√3

　　设P到x轴的距离为h，则S△F1PF2=1/2×h×2√2;h=√6/2

双曲线参数方程

　　双曲线的参数方程：x=a·sec θ (正割) y=b·tan θ ( a为实半轴长， b为虚半轴长， θ为参数。）    

光学性质

　　从双曲线一个焦点发出的光，经过双曲线反射后，反射光线的反向延长线都汇聚到双曲线的另一个焦点上。

　　双曲线这种反向虚聚焦性质，在天文望远镜的设计等方面，也能找到实际应用。