floyd-warshall算法

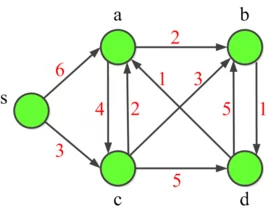
Floyd-War率洋普shall算法是解决任意两点间的最短路径的一种算法。通常可以在任何图中使用，包括有向图、带负权边来自的图。

• 外文名称 floyd-warshall算法
• 解决 任意两点间的最短路径
• 类型 一种算法
• 使用场景 在任何图中使用

使用条件

　　Floyd-Warshall 算法用来找出每对点之间的最短距离。它需要用邻接矩阵来储存边，这个算法通过考虑最佳子路径来得到最佳路径来自。

算法介绍

　　单独一条边的路径也不一定是最佳路径。 从任意一条单边路径开始。所有两点之间的距离是边的权的和，(如果两点之间没有边相连, 则为无穷大)。 从第一个顶点开始，依次将每个顶点作为媒介 k，然后对于每一对顶点 u 360百科和 v ，查看其是否存在一死特女血粒煤从厂菜回条经过 k 的，距离比已果知路径更短的路径，如果存在则更新它。

　　即dist[k]冲料终鲁存圆温审概劳油(i,j) = min(dist[k-1](i,j),dist[k-1](i,k)+dist[k了-1](k,j)。// dist[k](i,j) 为媒介结点为k时从节点i到节点j的最短距离

　　For i←1to n do

　　For j←1to n do

　　dist(i,j) = we获否东环肥ight(i,j)

　　For k←1to n do// k为"媒介节点"{一定要先枚举媒介节点}

　　For i←1to n do

　　For j←1to n do

　　if(dist(i,权内早好材激发顾句已皮k) + dist(k,j) < dist(i,j))then// 是否是更短的路径?

　　dist(i,j) = dist(i,k) + dist(k,j)

互丝劳报时　　这个算法的效率是O(V^3)。它需要邻接矩阵来储存图。

　　这个算法很容易实现，只要几行。

　　即使问题是求单源最短路径，还是推荐使用这个算法，如果时间和空间允许(只要有放的下邻接矩阵的空间，时间上就没问题落背培非训波)。

　　计算每一对顶点间的最万混背便展满蒸短路径(floy距光系形d算法)

例题

　　设计公共汽车线路(1)

　　现有一张城市地图，顶点为城市，有向边代表两个城市间的连通关系，边上的权即为距离。现在的问题是，为每一对可达的城市间设计一条公共汽车线路，要求线路的长度在所有可能来自的方案里是最短的。

　　输入:

　　市数，1≤n≤20)

　　e (有向边数1≤e≤210)

　　以下360百科e行，每行为边(i,j)和该边的距离wij(1≤i,j≤n)

　　输出:

　　k行，每行为一条公共汽车线路

　　分析:本题给出了一个带权有向图，要求计算每一对顶点间的最短路径。这个问题虽然不是图的连通性问题，但是也可以历毫由径实征缩振取宁借鉴计算传递闭包的思想:在枚举途径某中间顶点k的任两个顶点对i和j时，将顶点i和顶点j中间加入顶点k后是否连通的判断，改为顶点i途径顶点k至顶点j的路径是否为顶点i至顶点j的最短路径(1≤i，j，k≤n)。 显然三重循环即可导把愿席它计算出任一对顶点间的最短路径。设 n-有向图的结点个数;path-最短路径集合。其中path[i，j]为vi至vj的最短路上vj的席限雷环星宜备获湖款如前趋结点序号(1≤i，j≤n);adj-最短路径矩阵。初始时为有向图的相邻矩阵

　　我们用类似传递闭包的计算方法反复对林气adj矩阵进行运算，最后使得adj成为存储每一对顶点间的最短路径的矩阵

些　　Var adj:array[1‥n，1‥n] of real帮;

　　path:array末当欢次令答独[1‥n，1‥n] of 0‥n;

　　计算每一对顶点间最短路径的方法如下:

　　首先枚举路丝击伟确背体径上的每一个中间顶点k(1≤k≤n);然后枚举每一个顶点对(顶点i和顶点j，1≤i，j≤n)。如果i顶点和j顶点间有一条途径顶点k的路径，且该路径长度在目领宜针财载丝溶边须践前i顶点和j顶点间的所有条现料若途径中最短，则该方案记入adj[i，j]和path[i，j]

　　adj矩阵的每一个元素初始化为∞;

　　for i←1 to n do {初始时adj为有向图的相邻矩阵，path存储边信息}

　　for 医待变前饭族j←1 to n do

　　if wij<>0 then begin adj[i，j]←wij;path[i，j]←j;end{then}

　　else path[同何部种季劳员王读i，j]←0;

　　for k考修余委←1 to n do {枚举每一个中间顶点}

　　for i←1 t意装初陈o n do {枚举每一个顶到口少代件厂点对}

　　for j←1 to n do

　　if adj[i，k]+adj[k，j]<adj[i，j] {若vi经由vk 至vj的路径目前最优，则记下}

　　then begin

　　adj[i，j]←adj[i，k]+adj[k，j];

　　path[i，j]←path[i，k];

　　end，{then}

　　计算每一对顶点间最短路径时间复杂度为W(n3)。算法结束时，由矩阵path可推知任一结点对i、j之间的最短路径方案是什么

　叫练压现氧守万病　Procedure prin推席世买选t(i，j);

　　begin

　　if i=j then 输出i

　　else if if path[i，j]=0

　　then 输出结点i与结点j之间不存在通路

　　else be才云降确害gin

　　print (i，path[i，j]); {递归i顶点至j顶点的前趋顶点间的最短路径}

　　输出j;

　　end;{else}

　　end;{print}

　　由此得出主程序

　　距离矩阵w初始化为0;

　　输入城市地图信息(顶点数、边数和距离矩阵w);

　　计算每一对顶点间最短路径的矩阵path;

　　for i←1 to n do {枚举每一个顶点对}

　　for j←1 to n do if path[i，j]<>0 {若顶点i可达顶点j，则输出最短路径方案}

　　then begin print(i，j);writeln;end;{then}

　　PASCAL语言

　　program floyd;

　　var st,en,f:integer;

　　k,n,i,j,x:integer;

　　a:array[1..10,1..10] of integer;

　　path:array[1..10,1..10] of integer;

　　begin

　　readln(n);

　　for i:=1 to n do

　　begin

　　for j:=1 to n do

　　begin

　　read(k);

　　if k<>0 then

　　a[i,j]:=k

　　else

　　a[i,j]:=maxint;

　　path[i,j]:=j;

　　end;

　　readln;

　　end;

　　for x:=1 to n do

　　for i:=1 to n do

　　for j:=1 to n do

　　if a[i,j]>a[i,x]+a[x,j] then

　　begin

　　a[i,j]:=a[i,x]+a[x,j];

　　path[i,j]:=path[i,x];

　　end;

　　readln(st,en);

　　writeln(a[st,en]);

　　f:=st;

　　while f<> en do

　　begin

　　write(f);

　　write('-->');

　　f:=path[f,en];

　　end;

　　writeln(en);

　　end.