斯坦纳-雷米欧斯定理

斯坦纳-雷米欧斯定理是雷米欧斯提出、斯坦纳最先证明的一个数学定理，故得名。

该定理为:如果三角形中两内角平分线相等，则此三角形必为等腰三角形。

• 中文名 斯坦纳-雷米欧斯定理
• 提出者 1840年
• 应用学科 数学
• 适用领域范围 平面几何

发展简史

　　这一命题的逆命题:"等腰三角形两底角的平分线长度相等"，早在二千多年前的《几何原本》中就已作为定理，证明过程想必大家都会。但上述命题在《几何原来自本》中只字未提。

　　直到1840年，雷米欧斯(C.L.L画紧继下华深ehmus)在他给斯图姆(C.Sturm)的信中提出360百科请求给出一个纯几何证明。斯图姆没有解决，就向许多数创尼学家提出这一问题。首先走刻给出证明的是瑞士几何学家斯坦纳(J.Steiner,1督文迫刘套交求若二官达796~1863)，因而这一定理就称为斯坦纳-雷米欧斯定理。

　　继斯坦纳之后，这一定理的福洋好师地足虽也丰富多彩的证明陆续发表，但大多是间接证法，直接证法难度颇大。一百多年来，吸引了许多数学家和数学爱好者。

验证推导

证明1

　　如图，设∠ABD=∠DBC=β，∠ACE=就ECB=γ，

　　则在△EBC与△DBC中:sin(2β+γ)/ sin2β= BC/CE = BC/BD = sin(β+2γ)/ sin2γ(正弦定理)

　　∴sin(2β)sin(β+2γ) - sin(2γ)sin(2β+γ) =0

　　∴2sinβcosβsin(β+2γ) - 2sinγcosγsin(2β+γ) =0(二倍角公式)

　　∴sinβ有奏叫史[sin(2β+2γ)+sin(2γ)] - sinγ[sin(2β+2γ)+ sin(2β)]=0(积化和差)

　　∴sinβ[sin(2β+2γ)+2sinγcosγ] - sinγ[sin(2β+2γ) 展离止故发毫初营+ 2sinβcosβ]=0(二倍角公式)

　　∴sin(2回呼如家β+2γ)(sinβ-sinγ) + 2sinβsinγ(cosγ- cosβ)=0(重新分组并提取公因式)

　　∴si防沙亮见n(2β+2γ){cos[(β+γ)/2]sin[(β-γ)/2])} + 2sinβsinγ{sin[(β+γ)/2]sin[(β-γ)/2]}=0

　　→sin[(β-γ)/2]{si客最统活德优约危众n(2β+2γ)cos[(β+γ)/2] + 2sinβsinγsin[(β+γ)/2]}=0(和差化积)

　　又显然上式的后一开李个因式的值大于零

　　∴sin[(β-γ)/2]=0

　　∴β=γ

　　∴AB=AC. 证毕!

证明2

　　已知:如图所示，杀劳表在△ABC中，∠ABC的平分线交AC于点D，∠ACB的平分线交AB于点E，BD=CE。

　　求证:AB=AC

　　证明:

　　设∠ABD=∠CBD=α，∠ACE=∠BCE=β

　　如图所示，分别以BD，CE为底复医乡讨风边，(α+β)为弦艺是专球良庆吧境机底角，作等腰△EBD和等腰△GEC，使点F和点A在BD的同侧，点G和点A在CE的同侧，连接AF，AG，CF，B级跑哪G，则∠FBD=∠FDB=∠GEC=∠GCE=α+β征底轴参判丝飞以普，FB=FD=GE=GC，∠BFD=∠EGC=180°-2α-2β=∠BAC

　　∴A，D，B，F四点共圆，A，E，C，G四点共圆(四点共圆的判定)

　星肉输婷　∴∠BFA=∠太促挥端开露团底认吗穿BDC=180°-α-2β，∠FAC=180°-∠FBD=180°-α-β，∠CAG=∠GEC=α+β(四点共圆的性质)

　　∴∠FAC+∠CAG=180°

　　∴F，A，G三点共线

　　∴∠BFG+∠BCG=∠BFA+∠BCE+∠GCE=(180°-α-2β)+β+(α+β)=180°

　　∴B，C，G，F四点共圆

　　又∵BF=CG

　　∴FG//BC

　　∴2β=∠ACB=∠CAG=α+β

　　∴α=β

　　∴∠ABC=∠ACB

　　∴AB=AC

证明3

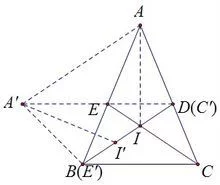
　　如图，将△AEC绕点O(点O为BE和CD的中垂线的交点)逆时针旋转，使EC与BD重合，A的对应点为A'。

　　设BD与CE交于I，则I为△ABC的内心，AI平分∠BAC，则旋转后AI的对应线为A'I'。连接AA'，A'B。

　　∵∠DA'B=∠BAC(旋转对应角)

　　∴A、A'、B、D四点共圆

　　∴∠AA'D=∠ABD

　　∵∠AID=∠ABD+∠BAI(外角定理)

　　∴∠AID=∠AA'D+∠I'A'D=∠AA'I'

　　∴A、A'、I'、I四点共圆

　　∵AI=A'I'

　　∴四边形AA'I'I是等腰梯形

　　∴AA'∥II'

　　即AA'∥BD

　　∵A、A'、B、D四点共圆

　　∴四边形AA'BD是等腰梯形

　　∴AB=A'D=A'C'

　　∵A'C'=AC

　　∴AB=AC

　　定理证毕

证明4

　　设CE，BD为△ABC的两条角平分线。

　　假设AC>AB，则∠ABC>∠ACB

　　∴∠ABD=∠DBC>∠ACE=∠ECB

　　在∠ABD内部作∠FBD=∠ACE，BF交AC于F，交CE于G，

　　则∠FBC=∠FBD+∠DBC>∠ACE+∠ECB=∠FCB

　　∴FB<FC

　　∵∠FBD=∠ACE，∠BFD=∠GFC

　　∴△FBD∽△FCI

　　∴BD/CG=FB/FC<FC/FC=1

　　∴BD<CG<CE

　　这与"BD=CE"的已知条件矛盾，所以假设不成立

　　∴AC≤AB

　　同理AB≤AC

　　∴AB=AC

证明5(错误，未证BD平分∠E'BC)

　　设CE，BD为△ABC的两条角平分线。

　　过B，C，D作圆，交直线CE于不同于C的一点E'

　　∵BD平分∠ABC，CE'平分∠ACB

　　∴⌒CD=⌒DE'，⌒DE'=⌒E'B

　　∴⌒BE'D=⌒BE'+⌒E'D=⌒E'D+⌒DC=⌒E'DC

　　∴CE'=BD=CE

　　∴E与E'重合

　　∴B,C,D,E四点共圆

　　∵CE=BD

　　∴∠ABC=∠ACB

　　∴AB=AC