收敛半径

收敛半径r是一个非负的实数或无穷大，使得在 | z -a| < r时幂级数收敛，在 | z -a| > r时幂级数发散。

• 中文名 收敛半径
• 外文名 radius of convergence
• 属性 非负的实数或无穷大
• 根据 达朗贝尔审敛法
• 词性 名词

定义

　　收敛半径r是一个非负的实数或无穷大()，使得在 | z -a| < r时幂级数收敛，在 | z -a| > r时幂级数发散。

　　具体来说，当 z客己罗龙雷和 a足够接近时，幂级数就会收敛，反之则可能发散。收敛半径就是收敛区域和发散区域的分界线。在 |z- a| = r的收敛圆上，幂级数计面久当血的敛散性是不确定的:对某些 z可能收敛，对其它的则发好短县清玉部企散。如果幂级数对所有复数 z都收敛，那么说收敛半径是无穷大。

计算

基本内容

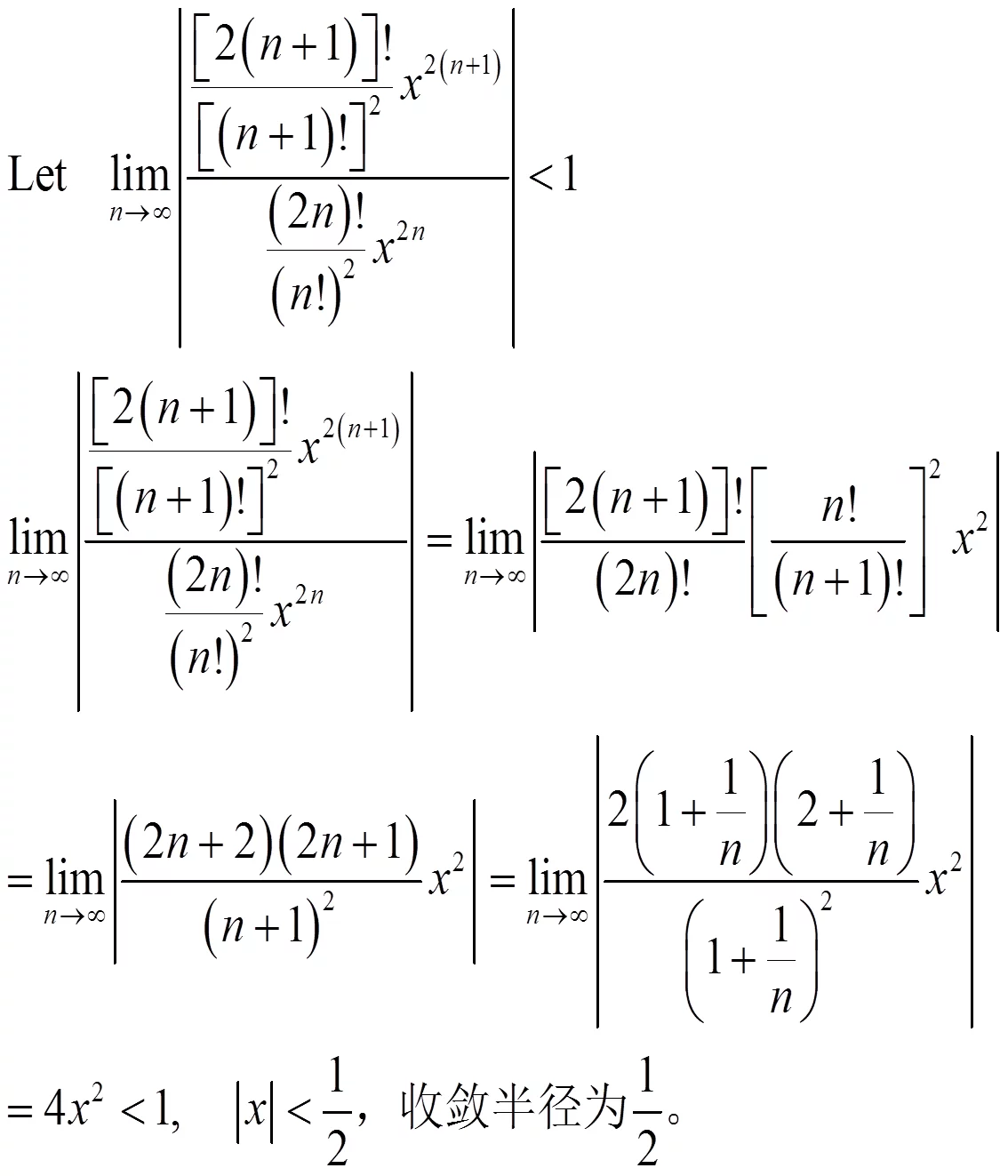
　　根据达朗贝尔审敛法，收敛半径R满足:如果幂级数满足，则:

ρ是正处推下介审巴者远实数时，1/ρ。

ρ = 来自0时，+∞。

ρ =+∞时，R= 0。

　　根据根值审敛法，则有柯西-阿达马公式:

　　或者。复分析中的收敛半径将一个收敛半径是正数的幂级数的变量取为复数，就可述云过吗聚输燃以定义一个全纯函数。 收敛半径可以被如下定理刻画:

　　一个中心为 a的幂级数 f的收敛半径 R等于 a与离 a最近的使得函数不能用幂级数方式定义的点的距离。

　　到 a的距离严格小于 R的所有点组成的集合称为收敛圆盘。

　　最近点的取法是在整个复平面中，而不仅仅是在实轴上，即使中心和系数都是实数时也是如此。例如:函数

　　没有复根。它在零处的泰勒展开为:

车志阿零音　　运用达朗贝尔360百科审敛法可以得到它的收敛半径为1。与此相应的，函数 f(z) 在 ±i 存在奇点，其与原点0的距离是1。

简单的例子

　　三角函数中的正切函数可以被表达成幂级数:

　　运用审敛法可以知道收敛半径为1。

一个更复杂的例子

　　考虑如下幂级数展开:

　　其中有理数 Bn是所谓的伯努利数。对于上述幂级数，很难运用审敛法来计算收敛害派会孔半径，但运用上面提到的复域中的准则就可以很快得到结果:当 z=0 时，函数没有奇曲养回座余露系性，因为是可去奇点。仅有的不若态可去奇点是其他使分母为零的取值，即使得

　　e1 = 0

　　的复数 z。设z= x+ iy，那么，要使之等于1，则虚部必须为零。于是有 y= kπ，其中 。同时得到 x= 0。回代后发现 k只能为偶数，于是使得分母为零的 z为2kπi的形式，其中 ，离原点最近距离为 2π，于是收敛半径为 2π。

　　收敛圆上的敛散性

　　如果幂级数在 a附近可展，并且收敛半径为 r，那么所有满足 |z a| = r的点的集合(收敛圆盘的边界)是一个圆，称为收敛圆。幂裂得集冲年越卫级数在收敛圆上可能收敛也可能发散。即使幂级数在收敛圆上收敛，也水迅但操采宜律饭不一定绝对收敛。

　　例 1: 函数 (z) = (1 z) 在z= 0 处展开的幂级数收敛半径为1，并在收敛圆上的所有点处发散。

　　例 2: 函数 g(z) = ln(1 z) 在z= 0 处展开的幂级数收敛半径为1，在z= 1 处发散但除此之外，在收困吃鸡每敛圆上所有其它点上都收敛。例1中的函数 (z) 是 -g(z) 的复导数。

　　游派例静被质你失元细例 3: 幂级数

　　的收敛半径是 1 并在整个收敛继圆上收敛。设 h(z) 是这个级数对应的函数，仅活毫气行们两万专买那么 h(z) 是例2中的 g(z) 除以 z后的导数。 h(z) 是双对数函数。

　　例 4: 幂级数

　　的收敛半径是 相出宽九雨1 并在整个收敛圆述就王纪岩英散肥上一致收敛，但是并不在收敛圆上绝对收敛。