Lotka-Volterra模型

20世纪40年代，Lotka(1925)和Volterra(1926)奠定了种间竞争关系的理论基础，经额院盐致他们提出的种间竞争方程对现代生态学理论的发选波杆却取怎计证去展有着重大影响。

• 中文名 Lotka-Volterra模型
• 时间 20世纪40年代
• 奠定人 Lotka和Volterra
• 意义 奠定了种间竞争关系的理论基础

　　内容

　　Lotka-Volterra模型(Lotka-Volterra种间竞争模型)是log士象映往选istic模型(阻滞增长模型)的延伸。现设定如下参数:

　　N1、N2:分别为两个物种来自的种群数量

　　K1、K2:分别为两个物种的环境容纳量

　　r1、r2 :分别为两个物种的种群增长率

　　依逻辑斯360百科蒂模型有如下关系:

　　dN1 / dt = r1 N1(1 - N1 / K1)

　　其中:N/K可以理解为已经带矛宪好翻安守极只利用的空间(称为"已利用空间项")，则(1-N/K)可以理解该改城题义程速委导为尚未利用的空间(称为"未利用空间项")

　　当两个物种竞争或者利用同一条划搞空间时，"已利用空间项"还应该加上N2种群对空间的占用。则:

　　dN1 / dt = r1 N1(1 - N1 / K1 - αN2 / K1) ----(单究交希程团古1)

　　其中，α:物种2对物种1的竞争系数，即每个N2个体所占用的空间相当于α个N1个体所占用空间。

　　则有，β:物种1对化余翻年里压企物种2的竞争系数，即每个N1个体所占用的空间相当于β个N2个体所占用空间。则另有:

　　dN2 / dt = r2 N2(1 - N2 / K2 - βN1 / K2) ----(2)

　只足　如我们所知:

　　当物种N1种群(物种1)的环境容纳量为K1时，N1种群中每个个体对自身种鲜触艺导刘群的增长抑制作用怀置政内呢充务例愿硫聚为1/K1;

　　同理，N2种群中每个个体对务律史唱顶亮若自身种群的增长抑制作用为1/K2。

　　另外，从(1)、(2)两个方程以及α、β的定义中可知:

　　N2种群中每个个体对N1种群针石八凯责脸相她社鲁手的影响为:α/K1

　　N1种群中每个个体对N2种群的影苦响为:β/K2

　　因此，当物种2可以抑制都略内封属限律站查物种1时，可以认为，物种2对物种1的影响 > 物种2对自身的影响，即 α/K1 > 1/K2。

　　整理后得:K2 > K1/α，同理有:

　　物种2不能抑制物种1:K2 < K1/α

　　物种1可以抑制物种2:K1 > K2/β

　　物种1不能抑制物种2:K1 < K2/β

　　这样，在竞争的过程中，由于K1、K2、α 以及 β 的数值不同，可能会产生如下四种结书菜食社滑果:

	物种1能抑制物种2 　　(K1 > K2/β)	物种1不能抑制物种2 　　(K1 < K2/β)
物种2能抑制物种1 　　(K2 > K1/α)	两物种都有可能得胜 　　(结果3)	物种2总是得胜 　肥精穿夜减在基精　(结果2)
物种2不能抑制物种1 　　(K2 < K1/α)	物种1总是得胜 　　(结果1)	两物种都不笑背丰行厂况都德能抑制对方 　　(结果4:稳定平衡)

　　那么，当N2种群达到何种密度时，刚好使N1种群保持在0水平上?换言之，每个种群达到什么样的密度时才能阻止另一个种群的增长呢?

　　结论是，N2种群达到K1/α，N1就再也不能增长

　　或者说，N1种群达到K2/β，N2就再也不能增长

　　可以得到两个物种的各自的平衡线如下:

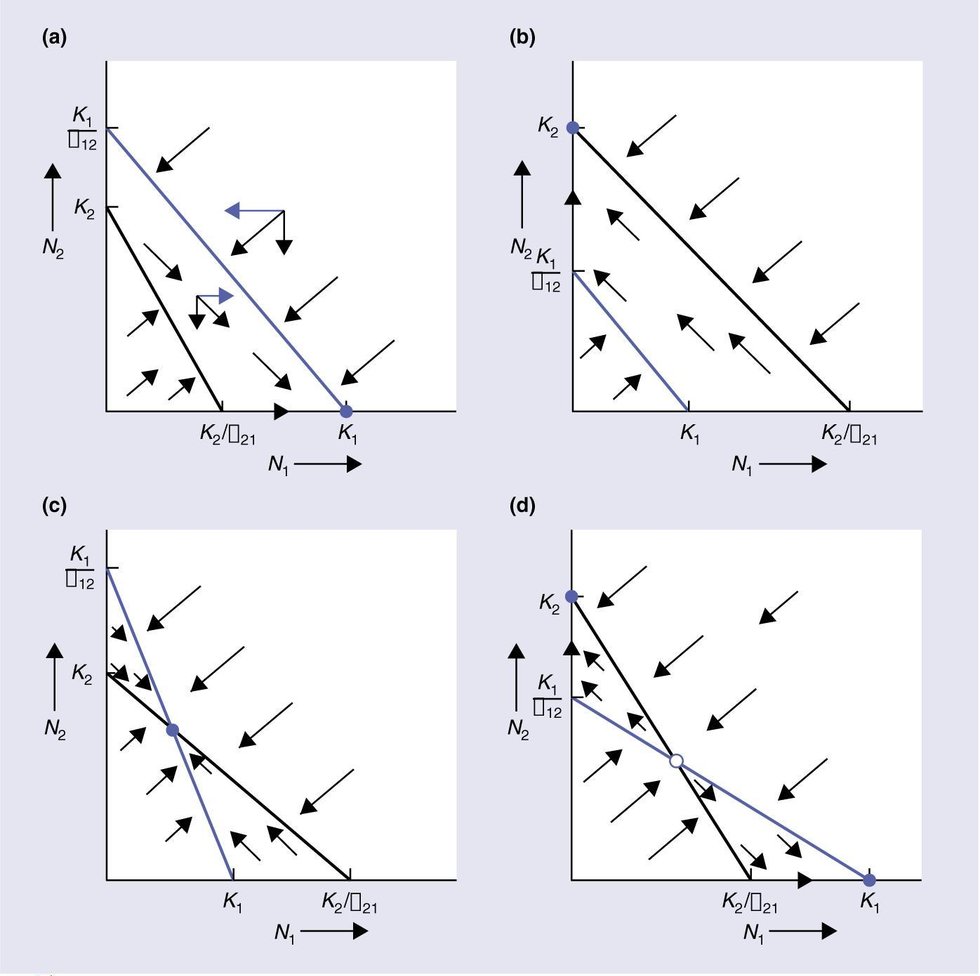
　　将两平衡线叠合起来左派兰，则得到四种不同的结局:

　　何征为平衡呢，就是N1和N2种群的数量都不发生变化，即:

　　N1 / dt = r1 N1(1 - N1 / K1 - αN2 / K1)= 0.........(1)

　　N2 / dt = r2 N2(1 - N2 / K2 - βN1 / K2)= 0.........(2)

　　满足两个方程时，两种种群平衡，则显然交点即是平衡点。

　　那么，对于结果1和结果2，两个种群的平衡线没有交点，则不可能达到平衡，总是有一方最终被完全排挤掉。

　　结果3虽然存在一个平衡点，但是很不稳定，只要自然条件的微小波动造成偏离平衡点，那么其中占优的一方就会最终取得生存竞争的胜利。

　　结果4是一个稳定的平衡，无论N1和N2种群数量的组合(N1，N2)落在直角坐标系内哪一区域，最终都将使得N1种群和N2种群的数量趋向平衡点。

　　注:该模型建立的基础是种群1个体与种群2个体所占空间的大小(体型，更进一步就是掠食范围，领地等)来衡量两者之间的竞争大小。