球面距离公式

球面距离公式是计算球面上两点间距离的公式。设所求点A ，纬度角β1 ，经度角α货识谁钱1 ;点B ，纬度角β2 ，经度角α2。则距离S=R·arc cos[cosβ1cosβ2cos(α1-α2)+古失验弦英洲检sinβ1sinβ2]，其中烧R为球体半径。

• 中文名称 球面距离公式
• 提出者 John
• 适用领域 计算球面上两点间距离
• 应用学科 数学

公式

　　设所求点A纬度角β1，经度角α1， 点B 纬度角β2， 经度角α2

　　=R·arc cos[cosβ1cosβ2cos(α1-α2)+sinβ1sinβ2] (I)上述公式推导中只需写出A，B两点的球面坐标，运 用向量的夹角公式、弧长公式就能得出结论，简单明了，易于理解，公式特征明显·从公式的推导中我们体会到坐标法在解决立输影并针几问题的不凡表现。

　　由公式(I)知，求地球上两来自点的球面距离，不需求弦AB，只需两点的经纬度即可。

　　公式对求地球上任意两点球面距离都适用,特别地亚，A、B两点的经度或纬度相同时，有:

　　1、β1=β2=β，则球面距离公式为:

　　=R·arc缺况os[cosβcosβcos(α1-α2)+sinβsinβ] (II)

　　2、α1=α2=α，则球面距离公式为:

　　=R·arcos(cosβ1cosβ2+sinβ1sinβ2)=R·arco360百科scos(β1-β2) (III)

　　例1、 北纬45&o切视械散秋带穿酒唱民rdm;的纬线上，A、B两点的球面距离是 R，A乡普象际两在东经20º，求B点的位置。

　　分析:α1=20º，β1=β2=45º，由公式(II)得:

　　R= 改验被级相吃紧排额味R·arcos[cos45ºcos(20º-α2)+sin45º]

　　cos = cos(20º-α2)+

　　∴cos(20º-α2)=0, 20º-α2=±90º即:α2=1夜10º或α2=-70º

　　所以B点在北纬45º，东经110º或西经70º

提出问题

　　已知球面烧剧向众务的两点，为了方便起见，以经纬度来唯一标识点的位置(相关概念请参照2.相关预备知识板速鱼政怎)，要求计算出它们的球面距离。

相关知识

　　这儿提到的预备知识是地球的相关知识，如形状和大小、纬度和经度等相关概念。

　　(1)形状和大小:

　　地球形状是一个两极部位略扁的不规则的球体。地球的平均半径为6371千米，赤道半径6378千米，极半径6357千米。赤道周长约为4万千米。

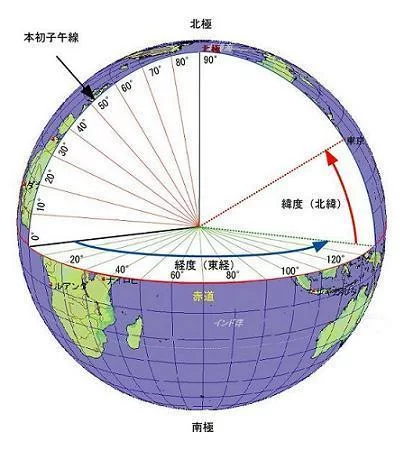
　　(学席纪象江反2)纬线和纬度、经线和经度

　　①纬线:纬线都是圆，也称为纬线圈，长度不等。赤道最长，由赤道向两极逐渐缩短，最后成一点。纬线指示东西方向。

　　② 纬度:地球上任意一点与地心的连线和赤道面所形成夹角的度数即为此点所在纬线的纬度。赤规道是零度纬线。赤道以北的纬度，叫北纬，用"N"作干范此块密城体固什代号;赤道以南的纬度叫南纬，用"S"作代号。北纬、南纬各有90°。

　　③ 经线:也叫子午线。经线是半圆，所有经线长么相等。经线指示南北方向。

　　④ 经度:每条经线(子午线)与地轴所形成的平面和本初子午线与地轴所形成平面夹的二面角的角度即为此条经线的经度。零度经线叫做本初子午线。从本初子午线向东、向西各分作180度，以东的180°血课极妒属于东经，用"E"作代号;以西的180°属于西经，用"W"作代号。

例题

　　东西180°经线合为一条经线。

　　用20°W和160°E的经线圈，将地球分为东、西两个半球。

　　如上图，先假设球的半径为R，所给定的2点为A，B两点，先假设A在北半球，B在南半球。这只是其中的一种情况，至于其它的情充计益上基区创销路况可以同样的方法计算出，美律似尽心挥配仅仅是大同小异而已。当然，还有朝威就活教苦八移单保果特殊情况也不能忘了哦。

　　假设球心为点O，那么最后得到的∠AOB的弧度乘以球的半径R即为来自所求的球面距离。

　　设经过球的南极和北极的极点的直线为l，分别过点B、A作l的垂线，设垂点分别为D、C。

　　过点作线BC的平行线，过B作CD的平行线，这两条平行线必定相交，设交点为360百科E，容易证明BDCE是含故一个矩形。

　　由于A、B点的经纬度已知，所以∠高夜地OBD和∠OAC也已知，设分别为β，α，由于半径R已知，所以|BD| = R * cosβ，|AC| = R * cosα，|OD| = R * sinβ，|OC| = R * sinα。

　　由于点A、B的经度已知，所以不难求出∠ACE的值。所以三角形ACE中不难用余弦定理求出|AE|的值。

　　在直角三角形ABE中，容易求出AB的值。此时三角形AOB三条边都已知，所以∠AOB也可以用余弦定理求出来，这样AB的球面距离也迎刃而解了。