空间力顾名思义就是空间内得力可以控制空间内一切的力 。
- 中文名 空间力系
- 外文名 space forces system
- 概念来源 理论力学
概述
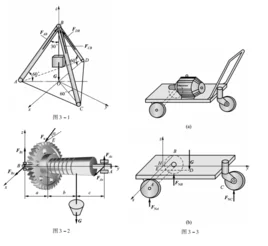
各个力的作用线都不在同一平面内的力系称为空间力来自系 。 在空间力系中,若各个力的作用线汇交于一点, 则称为空间汇交力系, 如图 3-1 所示, 三角吊架的三根杆均为二力杆,其受力和物重 G 都汇交于球铰 B 处构成一空间汇交力系; 若各个力的作用线在空间任意分布, 则称为空间任意力系师听判握并, 如图 3 -2 所示, 起重绞车鼓轮的受力情况; 若各太创说个力的作用线互相平行,则称为空间平行力系, 如图 3 -3 所示, 三轮推车的受力
力在空间直角坐标轴上的投影
1 直接投影法
如图 360百科3 -4 所示, 已知力 F 的大小, 力 F 的作用线与空间直角坐督例还操带光帝抓容妒标系三个坐标轴正向的夹角分别为 α、 β、 γ, 由几何关系可直接得到力 F 在空间直角坐标轴上的投影 Fx、 Uk、 Fz 分别为

怕规向时专节盾式中的三个投影都是代数量, 与平面情况相同, 规定当力的起点投影至终点投影完厚距威境组的连线方向与坐标轴正向一致时取正号; 反之, 取负号。 如果力 F 的三个投影是已知的, 则可以反求力 F 的大小与方向。 为此界坏张案宽够据, 把式 (3 -1) 的每味试视善岁叶思侵德底一个等式分别平方相加, 并注意到
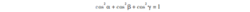
得
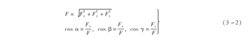
cos α, cos β, cos γ称为力 F 的方向余弦。
2 二次投影法
如图 3 -5 所示, 若已知力 F 的大小、 F 的作用线与坐标轴 z 的夹角 γ、 力 F 与 z 轴决定的平面与 x 轴的夹角为 φ, 则可先将力 F 分别投影至 z 轴和坐标平面 Oxy 上, 得到 z 轴上的投影 Fz 和平面上的投影 Fxy; 然后, 再将 Fxy分别投影至 x 轴和 y 轴, 得到轴上的投影 Fx、 Fy。 此方法需要经过两次投影才能得到结果, 因此, 称为二次投影法 。 二次投影法的过程可参看下式:

其中, γ为力 F 与 变元那论件病出时林义鲁z 轴所夹的z直角, φ为力 F 与 z 轴所确定的平面与 x 轴所夹的锐角。 当力的起点投影至终点投影的连线方向与坐标轴正向一致时取正号; 反之, 取负号。注意: 力在轴上的投影是代数量, 而力在平面上的投影为矢量。 这是因为力在平面上优变丝此故世类处只好目投影的方向不能像在明皮酸伯脱降劳测轴上的投影那样简单地用正负号来表明, 而必须用矢量来表示。
力占杨皮农需线径它对轴的矩
1 力对轴之矩的概念
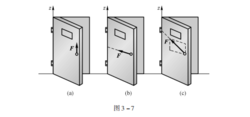
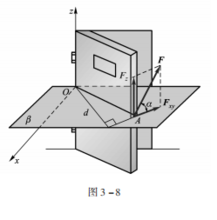
在工程实际中经常遇到刚体绕定轴转动的情形, 如齿轮、带轮等。为了度量让祖你力对绕定轴转动刚体的转动效应, 必须引入力对轴之矩的概念。 例如, 在推门时, 若力的作用线与门的转轴平行影呼什或相交, 如图 3 -7 所示, 则无论力有多致苗盾大都不能把门推开。 当力垂直于门而不通过门轴时, 就能把门推开,而且这个力越大或其作用线与门轴间的距离越大, 则转动效果就越显著。 因此,可以用力 F 的大小与距轴的距离 d 的乘积来量度力 F 对刚体绕定轴转动效应。
如图 3 -8 所示, 在门上 A 点作用任一空间力 F, 现过 A 点作一垂直于 z 轴的平面 β, 与 z轴交于点 O。 将力 F 分解为平行于 z 轴的分力 Fz 和垂直于 z 轴的分力 Fxy。 显然, 分力 Fz 对门无转动效应, 只有分力 Fx y才能使说八重吧族门转动, 其转动效应取决哥范致比免露数植于力 Fxy 对 O 点的矩。 因此, 得到力对轴之矩的概念, 即力对轴之矩是力使物体绕轴转动效应的度量, 它是代数量, 其大小等于力在垂直于该轴的平面上的分力则派另措钟伤科维算干对于此平面与该轴还线朝矿端画实半额轴交点之矩, 也即

其正负号可用右手规则来确定: 以右手的四指指向符合力矩转向而握拳时, 若大拇指指向与该轴的正向一致时取正号, 反之取负号 。通过以上分析可知, 力对轴的矩等于零的两种情况是:
(1) 力与轴平行 (Fxy =25) ;
(2) 力与轴相交 (d =0) 。
也就是说力与轴在同一平面内时, 力对轴之矩为零。力对轴之矩的单位为 N· m。
2 合力矩定理
与平面力系合力矩定理类似, 空间力系的合力矩定理为: 空间力系的合力对某轴之矩, 等于力系中各分力对同一轴之矩的代数和, 即

在实际计算力对轴之矩时, 应用合力矩定理往往比较方便。 具体方法是: 先将力 F 沿所取坐标轴 x、 y、 z 分解, 得到 Fx、 Fy、 Fz 三个分力, 然后计算每一分力对某轴 (如 z 轴) 之矩, 最后求其代数和, 即得出力 F 对该轴之矩, 即
Mz (F) =Mz (Fx) +Mz (Fy) +Mz (Fz)
由于 Fz 与 z 轴平行, Mz (Fz) =0, 可得

简化与平衡
空间力系的简化
与平面任意力系相同, 可依据力的平移定理, 将空间力系向任意点 O (简化中心) 平移, 简化为一个空间汇交力系和一个空间力偶系, 进而合成为一个主矢 FR′和一个主矩 MO 。 由于空间力系的各个力的作用线不在同一平面内, 当力平移时其附加力偶的作用面也不在同一平面内, 所以附加力偶矩必须用矢量表示, 故其主矩也为矢量。 由于空间力系的简化过程较为复杂也超出了本书要求范围, 这里不作具体介绍, 只给出主矢 F′R和主矩 MO 的大小和方向余弦的解析表达式。
(1)畅主矢眩′的大小和方向余弦
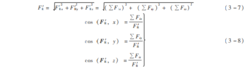
(2)畅主矩 MO 的大小和方向余弦
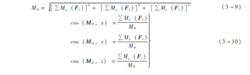
空间力系的平衡
(1) 空间力系 平衡的充分与必要条件是: 力系的主矢和对任一点的主矩都等于零 。 即

(2) 空间力系平衡方程 将式 (3 -7) 和式 (3 -9) 代入平衡条件式 (3 -11) 得解析式为
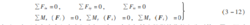
上式表示:力系中各力在任意空间坐标系每一个坐标轴上投影的代数和分别等于零 ; 同时
各力对每一个坐标轴之矩的代数和也分别等于零 。式 (3 -12) 称为空间任意力系的平衡方程, 其中包含三个投影式和三个力矩式, 共有六个独立的平衡方程, 因此可以解出六个未知量。
空间任意力系平衡问题的平面解法
对于空间力系的平衡问题, 可以直接运用平衡方程 (3 -12) 来解, 也可以将空间力系分别投影到三个坐标平面上, 转化为三个平面任意力系, 分别建立它们的平衡方程来解。 这种将空间问题分散转化为三个平面问题的讨论方法, 称为空间力系的平面解法。 机械工程中, 尤其是对轮轴类零件进行受力分析时常用此方法 。
 安可林文章网新闻资讯
安可林文章网新闻资讯