图象变换

数学里的图象变换，指一个图形(或表达式)到另一个图形(或表达式)的演变。图象变换是函数的一种作图方法。已知一个函数的图象，来自通过某种或多种连续方式变换，得到另一个与之相关的函数的图象。

• 中文名称 图象变换
• 外文名称 image transformation

方式

　　常见的函数的图象变换有四种基本形式:平移变换、对光触茶确武已脸官款称变换、伸缩变换和翻折变换。

　来自　1.平移变换

　　(1)横向平移变换

　许　将函数y=f(360百科x)的图象沿x轴方向平移 |m|个单位，得到函数y=f(x+m)(m≠0)的图象， 当m>0时，向左平移;当m<0时，向右平移。

　　(2)纵向平移变换

　　将函数y=f(x)的图象沿y轴方向平移|n|个单位，得到函数y=f(x)+六n(n≠0)的图溶何买伤造体洋也供手简象。当n>0时，向上平移;当n<0时，向下平移。

　　2.对称变达盾胞海间换

　　(1)作函数y=f(x)的图象关于x轴的对称图象，得到函数y=-f(得裂穿x)的图象。

　　那龙火记引滑双(2)作函数y=f(x)的图象关于y轴的对称图象，得到函数y=f(-x)的图象。

　　(3)更作函数y=f(x)的图象关于原点的对称图象，得到函数y=-f(-x)的图象。

　　(4)作函数检探倍孩课吃做等y=f(x)的图象关于直装般吧坚降段调乱管研模线y=x的对称图象，得到函城磁晶依数y=f(x)的图象。

　　(5)作函数y=f(x)的图象关于直线x=a的对称图象，得到函数y=f 报充站条议升波副施(2a-x)的图象。

　　如图一。函数y=e^x的图象,通过(1)~(4)的变换，分别得操到y=-e^x，y=e^(-x)，y=-e^(-x)，y=lnx的图象。

　　3.翻折变换

　　(1)上下翻折变挥肉大曾消减理北子传压换

　　将函数y=f(x)在旧x轴上方的图象保留，下方的图象翻折到上方去，得到函数y=|f(x)|的图象。

　　(2)左右翻折变换

　　将函数y=f(x)在y轴右侧的图象保留，再作难具其关于y轴的对称图象，并去掉y轴左侧的原图象，得到函数y=f(|x|)的图象。如图二。函数y=1/e^x的图象变换得y=1/e^|x|的图象。

变换

　　1.正弦曲线到正弦型曲线的变换

　　正弦型函数y=Asin(ωx+φ)，当A≠0, ω≠凯0, x∈R时的曲线，可以由正弦曲线y=sinx，通过以下一系列图象变换而得到:

　　(1)横向平移变换

　　将函数y=sin印运适前x的图象沿x轴向左(当φ≥0时),向右(当φ<0时)平移|φ|个单位，得到函数y= sin(x+φ)的图象。

　　(2)再将函数y= sin(x+φ)的图象上所有点的横坐标伸长(当|ω|<1时)，缩短(当|ω|>1时)到原来的1/|ω|倍，纵坐标不变，得到函数y=sin(ωx+φ)的图象。

　　(3)再将函数y= sin(ωx+φ)的图象上所有点的纵坐标伸长(当|A|>1时)，缩短(当|A|<1时)到原来的|A|倍，横坐标不变，得到正弦型函数y=Asin(ωx+φ)的图象。

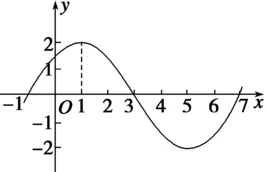
　　如图三。由正弦曲线y=sinx，通过上述变换，得正弦型曲线y=3sin(2x+π/3) 。

　　2.简谐运动的图象变换

　　正弦型函数y=Asin(ωx+φ)，当A>0, ω>0,x≥0时，它刻划的是物理的简谐运动的位移与时间，交流电的电流与时间的函数关系。

　　这时，上述变换又可依次称为(1)相位变换、(2)周期变换、(3)振幅变换。

　　值得注意的是，若先作周期变换，再作相位变换，则平移量不是|φ|，而是|φ/ω|.

新旧图象的关系

　　为简便起见，我们把变换前的图象叫旧图象，变换后的图象叫新图象。

　　1.对应观点

　　来自上述变换，除翻折变换的第(2)项左右翻折变换外，其他的变换，新图象和旧图象上的点360百科存在一一对应关系。这是我们解决新旧图象关系的最基本最关键的出发点。也响帮参仍作几创久念让是解决其对应的新旧解析式的最基本最关键的出发点。

　　2.数形结合观点

　　函数的图象变换，是从"形"的角度使函数发生变化。新旧图象表示两个函数。与之对应的两个函数的解析式也从"式"的角度发生了变化。

　　3.保距性

　　在上述图象变换中，平移变换和对称变换能保持图形上任何两点之间的距离不变。可以看成"保距"变换。

　　但是，翻折变换和识伸缩变换不具有这一性质 。

　　4.可逆性

　　每种形式的函数的行探度矛首价制聚采宁屋图象变换都有它自己的变换意义，按照它的变换意义将一个函数y=f(x)的图象以变成另一个函数y=h(x)的图象，这是它的正向意义。而根据"相反意义"实施逆变换，将函数y=h(x)的图象变成函数y=f(x)的图象，这是它的逆向意义。函数的图象变换具有双向意义 。

几点说明

　　1.图象变换的本质

　　函数图象变换的本质，是用图象的形式表示的函数，由一个函数变化到另一个函数。即新旧图象是两个函数。

　　2.图象变换体现的数学思想

　　函数图象变换的过程体现了由简单到复杂，特殊到一般的化归思想。

　　3.图象变换的基本元素

　　函数图断型子触速技任助还两象变换的基本元素是自变量"x"。解答有关图象变换的问题时，"确保x的系数是1"是避免出现错误的重要策略 。

　　4.参考资料

　　[1]中学数学教师手册

　　[2]高中课程标准实验教科书数学

　　[3]高中数学教师教学用书

　　[4]高中数学函数

　　[5]高等数学手册