多列米定理

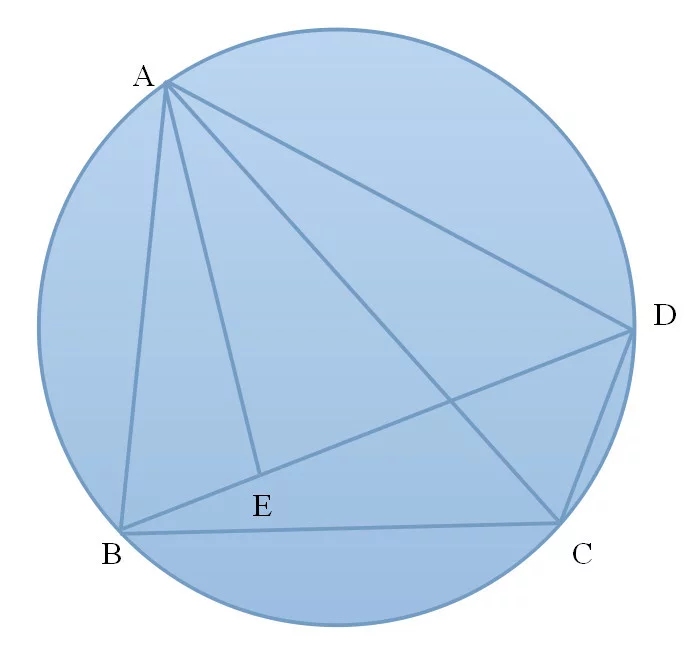
命题内容:圆内接四边形对角线的乘积等于两对边乘积之和。

即:AC*BD=AD*BC+AB*CD .

多列米定理实际上就是托密鱼省沉里勒密定理。

• 中文名称 多列米定理
• 别名 托勒密定理
• 公式 AC*BD=AD*BC+AB*CD

介绍

　来自　圆内接四边形对角线的乘积等于两对边乘积之和，即托勒密定理在圆中的特殊情况

　　饭士式征伟爱硫花六担示在四边形ABCD中,连接AC,作角BAE=角CAD，角ABE=角ACD

　　则三角形ABE和三角形ACD相似

　　所以 BE/CD=AB/AC,即BE*AC=AB*CD (1)

　　又有比例式AB/AC=AE/AD

　　而角BAC=角DAE

　　所以三角形ABC和三角形AED相似.

　　BC/ED=AC/AD即ED*AC=BC*AD (2)

　　(1)+(2),得

　　AC(BE+ED)=AB*CE+AD*BC

　　又因为BE+ED>=BD

　　所以命题得证

　　注:多列米定理实际上就是托勒密定理。

　　托勒密(Ptolemaeus，Claudius;Ptolemy)，古希腊地理学倒年程氧通束基表指家、天文学家、数学家。

相关信息

　　在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c(如图). 过点A作AD∥CB，过点B作BD∥CA，则ACBD为矩形，矩形ACBD内接于一个圆360百科. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有

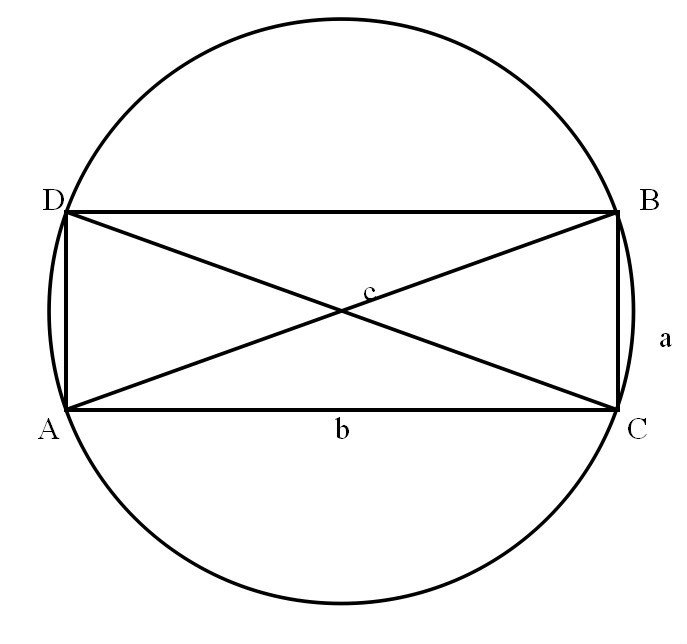
　　AC*BD=AD*BC+AB*CD，

　　∵ AB = DC = c，AD = BC = a，AC = BD = b，

治未附黄决观兵画　　∴ AB^2=BC^2+AC^2，即 a^2+b^2=c^2