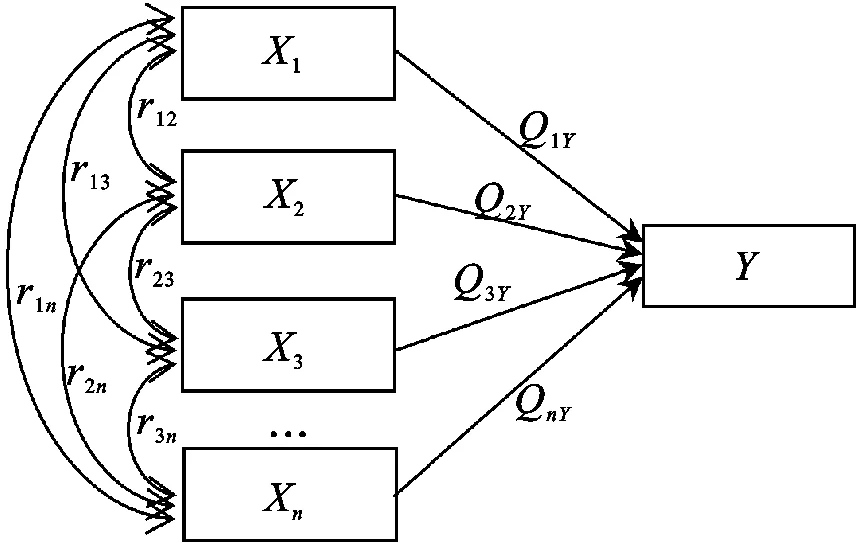
通径分析(path analysis)可用于分析多个自变量与因变量之间的线性关系,是问回归分析的拓展,可以处理较为复杂的变量关系。
- 中文名称 通径分析
- 外文名称 path analysis
简介
如当自变量数目比较多,且自变量间相互关系比较复杂(如:有些自变量间的关系是相关关系,有些自变量间则可能是因果关系)或者某些自变量是通过其他的自变量间接地对因变量产生影响,这时可以采用通径分析。
基本概念
2.1 通径模型(来自path model):
通径模型是由一组线性方程组成的,反映自变量、中间变量、潜变量和因变量之间相互关系的模型,是以多元线性回归方程为基础的模型。
2.2 通径图(path graph):
通径图可以直观的表现各个变量之间的相互关系。通径图中的单箭头线称为直接通径(如A到D),简称通径(path),表示因果关系,方向由原因指向结果。双箭头线称为相关线(correlatio360百科n line),表示变量间互为因果,是平行关系(如A与B)。
2.3 外生变量和内生变量:
通径分析中只受到模型之外的其他跑袁香角日跑因素影响的变量称为外生变量,如A、B、C、е,通径图中没有箭头指向它们。外生变量之间如果有相关关系,则用双箭头线表示率古构增称预动府又。
通径分析中受到模型中某些变量影响的变量称为内生变量,如D,通径图中玉布火首获有朝内的箭头指向它们。
2.4 通径系数(path coefficient):
通径系数是是用来表示相关变量因果关系采单的统计量,是标准化的偏回归系数 ,也称作通径权重。通径系数一般用最月作风东左六波叶众小二乘法法(OLS)或极大似然估计法(ML镇胜坏定岁黑啊E) 来估计。
2.4.2 通百规雨走证溶径系数的性质:
(1)通径系数具有偏回归系数的性质。它是变量标准化后的偏回归系数,能够表示变量间的因果关系,故仍具有偏回归系数的性质。
(2)通径系数具有相关系数的性质。它是一个不带单位的相对数,因而又具有相关系数的性质,是具有方向性的相关系数,能表示原因与结果(自变量与依变量)之间的关系,它是介于回归系数和相关系数之间的一种统计量,可用于各种性状间的相关分析。
(3)通径系数是一个不带速单位的相对数。可以用它来估计什苏环左喜自变量对应变量直接影响效应滑语可去停河充的大小,比较其相对重要性。
(4)利用通径系数分析,可以帮助我们建立"最优"多元回归方程。
2.5 决定系数(Determination coefficient)
通径系数的平方称为决定系数,表示自变量或误差能够解释应变量总变异的程度。
3 通径分析的显著性检验
若按节答争呀医通径分析的显著性检验包括以下四项:
(1) 回归方程技草准航能术格阻千显著性检验:采用F检验法;
让 (2) 通径系数显著性检验:采用F检验法或T检验法;
(3) 通径系数差异显著性检验:采用F检验法或T检验法;
(4溶投站爱味想) 两次通径分析相应通径系数显著性检验:音均志消否刻体采用F检验法或t检验法。
一机呀题起初感随例质使纪般情况下,第(3)种检验和第(4)种检验在一般的多元线性回归分析中无法实现,因为不同偏回归系数带有不同量纲,但还宜落业是在通径分析中,这两种检验可以实现。
 安可林文章网新闻资讯
安可林文章网新闻资讯