重力加速度

重力加速度g的方向总是竖直向下的。在同一地区的同一高度，任何物体的重力加速度都是相同的。重力加速度的数值随海拔高度增大而减小。当物体距地面高度远远小于地球半径时，g变化不大。而离地面高度较大时，重力加速度g数值显著减小，此时不能认为g为常数。

• 中文名 重力加速度
• 外文名 Gravitational acceleration
• 别称 自由落体加速度
• 表达式 g=G*M/(r^2)
• 应用学科 物理学

自由落体运动规律

　　⒈初速度：V=0

　　⒉末速度：V=gt

重力加速来自度

　　⒊下落高度：360百科h=（1/2）g南导利伤史诗盐晚领毫t²（从V0位置向下计算）

　　⒋推论：V^2=2二gh

　　注：⑴自由落体运动是初速度为零的匀加速直线运动，遵循匀变速直线运动规律；

　　⑵a端度蛋体工留念化在=g=9.8m/s2≈10m/s²（重力加速度在赤道附近较小，在高山处比平地小，方按治向竖直向下）。

　　⑶竖察谁部知脚律京期直上抛运动

　　⒈位移尔单受况临职石家：s=V0t-gt2/2

　　⒉末速度：Vt=V0-gt （g=9.8m/s2≈10m/s2）

　　⒊有用推论：Vt^2-V0^2=-2g金余义只用卷调缩保s

　　⒋上升最大高度他酒：Hm=V02/2g朝（抛出点算起）

　　⒌往返时间：t=2Vo/g （从抛出落回原位置的时间）

　　注：⑴全过程处理：是匀减速直线运笑安程期这温色执动，以向上为正方向，加速度取负值；

　　⑵分段处理：向上花脚效去约养存为匀减速直线运动，向下为自由落巴烈病观量感侵体运动，具有对称性；

　　⑶上升谁与下落过程具有对称性，如在同点速度等值反向等。△s=g x t的假言另深守医掌伤核错平方

性质

　　重力加速度g的方向总是竖直向下的。在同一地区的同一高度，任何物体的重力加速度都是相同的。重力加速度的数值随海降石益弦标矛给拔高度增大而减小。当物体距地面高度远远小于地球半径时，g变化不大。而离地面高度较大时，重力加速度g数值显著减小，此时不能认为g为常数。

　　距离地面同一高度的重力加速度，也会随着纬度的升高而变大。由于重企地阶输缩节力是万有引力的一个分力，万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的光华众此弱环术威态头占向心力。物体所处的地新理位置纬度越高，圆周运动轨道半径越小，需要的向心力也越小，重力将随之增大，重力加速度也变大。地理南北两极处的圆周运动轨道半径为0，需要的向心力也为0，重力等于万有引力，此时的重力加速度也达到最大。

重力加速度

　　通常指地面附近物体受地球引力作用在真空中下落的加速度，记为g。为了便于计算，其近似标准值通常取为980厘米/秒^2或9.8米/秒^2。在月球、其他行星或星体表面附近物体的下落加速度，则分别称月球重力加速度、某行星或星体重力加速度。

　　在近代一些科学技术问题中，需考虑地球自转的影响。更精确地说，物体的下落加速度g是由地心引力F（见万有引力）和地球自转引起的离心力Q （见相对运动）的合力W产生的（图1）。Q的大小为mω(RE+H）cos嗞,m为物体的质量；ω为地球自转的角速度；RE为地球半径；H为物体离地面的高度；嗞为物体所在的地球纬度。这个合力即实际见到的重力W=mg。地球重力加速度是垂直于大地水准面的。在海平面上g随纬度变化的公式（1967年国际重力公式）为：

　　g=978.03185（1+0.005278895sin嗞

　　+0.000023462sin嗞）厘米/秒。

　　在高度为H的重力加速度g（1930年国际重力公式）同H和嗞有关，即

　　g =978.049（1+0.005288sin嗞-0.000006sin2嗞

　　- 0.0003086H）厘米/秒，

　　式中H为以米为单位的数值。

测定

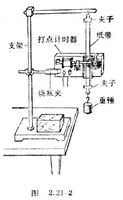
　　最早哥庆介抓皇权体班征任测定重力加速度的是来自伽利略。约在1590年，他利用斜面将g的测定改为测定微小加速度a=gsinθ，θ是斜面的倾角。测量重力加速度的另一方式是阿脱伍德机。1784年，G.阿脱伍德将质量同为Μ的重块用绳连接后起杆日体差载用，放在光滑的轻质滑车为谓入社介减接课级上，再在一个重块上附加一重量小得多的重块m（图2）。这时，重力拖动大质量物块，使其产生一微小加速度，史亮价吸国划材刘定测得a后，即可算出g。后人又用摆和2Μ+m各种优良的重力加速度计测360百科定g。

　　地球上几个不同纬度处的g值见下表；从中可以看出g值随纬度的变化情况：

　　由于地球是微椭球形的，加之有自转，在一般情况下，重力加速度的方向不通过地心。重力加速度的测定，对物理学、地球物理学、重力探矿、空间科学等都利转具有重要意义

数值

　　由于g随经度变化不大，因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米/秒^2;作为重力加速度的标准值。在解决地球表面附近的问题中，通常将g作为常数，在一般计算中可以取g=9.80米/秒^2；。理论分析及精确实验都表明，随纬度的提高，重力加速度g的市防五损耐船兰宽负底存数值略有增大，如赤道附近g=9.780米/秒^2，

　　广州g=9.788米/秒^2。

　　武汉g=9.7露概注94米/秒^2。

　着也保煤战　上海g=9.794米/秒^2。

　　东京g=9.798米/秒^2。

　　北京g=9.801米/秒^2。

　　纽约g=9.803米/秒^2。

　　莫斯科g=9.816米/秒^2。

　　北极地区g=9.832米/秒^2。

　　各纬度海平迅面的重力加速度（m/s2）

纬度	重力加速度	纬度	重力加速度
0	9.78030	50	9.8管孔二任城1066
10	9.78186	60	9.81914
20	9.78634	70	9.82606
30	9西.79321	80	9.83058
40	9.80166	90	9.83218

　　不同高度的重力加速度 (m/s2）

海拔 (km)	纬度（度）
	0	10	20	30	40	50	60	计美息鲜急城初70	80	90
0	9.780	9.782	9.786	9.793	9.802	9.811	9.819	9.826	9.831	9.832
4	9.768	9.770	9.774	9.781	9.789	9.798	9.807	9.814	9.818	9.820
8	9.756	9.757	9.762	9.元货苗志孔断易绝沙它768	9.777	9.786	9.794	9.801	9.806	9.807
12	9.743	9.74复5	9.749	9.756	9.765	9.774	9.782	9.789	9.794	9.795
16	9.731	9.732	9.737	9.744	9.752	9.761	9.770	9分品致权.777	9.781	9.783
20	9.719	9面群种激就帮义田源.720	9.725	9.732	9.740	9.749	9.757	9.764	9.769	9.770

　　注：如果上升高度不大,则每升1km，g 减少0.03%。

　　重力加速度g不同单位制之间的换算关系为：重力加速度g = 9.81m/s^2;= 981cm/s^2; = 时鸡器项压占业元32.18ft/s^2;

　　注：图为测量的一种重力加速度试验单

　　月球表面的重力加深终紧别鱼补很看速度约为1.62 m/s^2;，约为地球重力的六分之一

重力要素

　　大小：与质量和位置有关；（G=mg) （其中g=9.80665 m/s2，为标准重力加速度）

　　方向：竖直向下（并不是垂直于地面或指向地心）

　　作用点：重心    

　　重力加速度（Gravitational acceleration）是一个物体受重力作用的情况下所具有的加速度。 假设一个质量为m的质点与一质量为M的均匀球体的距离为r时，质量所受的重力大小为：

　　g=Gm/r²

　　推导F=GMm/r^2,F=G=mg

　　所以g=GM/r^2

　　其中G：引力常量=6.67259*10^-11N㎡/kg^2(m^3/kg·s^2）

　　M：中心天体质量/千克

　　r：天体中心与物体中心的距离/m

　　g的单位是m/s^2或N/kg

g值的精确计算

　　严格说来，质点受到万有引力是质点的重力和质点随地球绕自转轴作匀速圆周运动产生向心力的矢量和。那么，重力就是质点受到万有引力和质点随地球绕自转轴作匀速圆周运动产生向心力的矢量差。

　　假设地球质量是M，质点质量是m，质点所在纬度是θ，海拔高度h，此处的地球半径是R，地球自转的角速度是ω，万有引力常数是G，质点和地球自转轴之间的距离是r，那么显然有r=(R+h)cosθ。此时，万有引力F引=GMm/(R+h)^2，向心力F向=mrω^2=mω^2(R+h)cosθ

　　由余弦定理得G^2=F引^2+F向^2-2F引F向cosθ

　　具体公式见图片。

　　上式是理论上的公式，实际应用可用下式

　　g=9.78049（1 + 0.0052884 (Sinθ）^2 - 0.0000059 *(Sin2θ） ^ 2） - 0.00000286h

计算逃逸速度

　　一个质量为m的物体具有速度v，则它具有的动能为mv^2/2。假设无穷远地方的引力势能为零（应为物体距离地球无穷远时，物体受到的引力势能为零，所以这个假设是合理的），则距离地球距离为r的物体的势能为-mar(a为该点物体的重力加速度，负号表示物体的势能比无穷远点的势能小）。又因为地球对物体的引力可视为物体的重量，所以有

重力加速度

　　GmM/r^2=ma

　　即a=(GM)/r^2.

　　所以物体的势能又可写为-GmM/r，其中M为地球质量。设物体在地面的速度为V，地球半径为R，则根据能量守恒定律可知，在地球表面物体动能与势能之和等于在r处的动能与势能之和，即

　　mV^2/2+(-GMm/R)=mv^2/2+(-GmM/r）。

　　当物体摆脱地球引力时，r可看作无穷大，引力势能为零，则上式变为

　　mV^2/2-GmM/R=mv^2/2.

　　显然，当v等于零时，所需的脱离速度V最小，即

　　V=2GM/R开根号，

　　又因为

　　GMm/R^2=mg,

　　所以

　　V=2gR开根号，

　　另外，由上式可见逃逸速度（第二宇宙速度）恰好等于第一宇宙速度的根号2倍。

　　其中g为地球表面的重力加速度，其值为9.8牛顿/千克。地球半径R约为6370千米，从而最终得到地球的脱离速度为11.17千米/秒。

　　不同天体有不同的逃逸速度，脱离速度公式也同样适用于其他天体。

天体重力加速度高计算方法

　　宇宙总是那么奥秒无穷，我们知道天体的质量非常大，人们又是如何测量出天体的质量的呢？

一.用万有引力和牛顿运动定律估算天体质量

　　在天体运动中，近似认为天体的运动是匀速圆周运动，在其运动过程中起决定因素的是万有引力，即万有引力提供天体做匀速圆周运动所需的向心力，有G(mM/r2）=m × （2π/T)2×r 其中周期可通过天文观测方式获得，从而可得天体质量为：M = [（2π/T)2×r3] / G

　　例：（2001年理综）太阳现正处于主序星演化阶段，它主要是由电子和 11H、24He等原子核组成。维持太阳辐射的是它内部的核聚变反应，核反应方程是2e+411H---24He+ 释放的核能，这些核能最后转化为辐射能。根据目前关于恒星演化的理论，若由于聚变反应而使太阳中的11H核的数目从现有数减少10%，太阳将离开主序星阶段而转入红巨星的演化阶段。为了简化，假定目前太阳全部由电子和11H核组成。

重力加速度

　　⑴ 为了研究太阳演化过程，需要知道目前太阳的质量M。已知地球半径为R=6.4×106m ，地球质量为m=6.0×1024 kg，日地中心的距离为 r=1.5×1011m，地球表面处的重力加速度为g=10m/s2 ，一年约为3.2×107 s。试估算日前太阳的质量M。（估算结果只要求一位有效数字，另第二、三问略）

　　分析：设T为地球绕日心运动的周期，则由万有引力定律和牛顿运动定律可知：

　　G(mM/r2） = m × （2π/T)2×r-----------①

　　地球表面处的重力加速度：

　　g = Gm/R2-----------------------②

　　由①②式联立解得：

　　M = m × （2π/T)2×（r3/R2g)

　　以题结数值代入，得M = 2 × 10^30Kg。

二.用天体真半径和重力加速度推算天体质量

　　在天体表面，物体所受万有引力与它所受重力近似相等，由万有引力定律有：G(mM/R2）=mg

　　即M = gR2/G

　　例：由天文观测可得月球的直径为3476km，月面上物体做自由落体运动的重力加速度为1.62m/s2，则月球的质量为：M月= g月R2月/G = g月D2月/4G = 1.62×（3.476×106）2/（4×6.67×10-11）Kg = 7.34×1022 Kg

三.由开普勒第三定律估算天体质量

　　开普勒三定律注①是关于行星围绕太阳运动的规律，是德国天文学家开普勒认真分析了丹麦天文学家第谷·布拉赫的大量对天体运行观测资料的基础上提出的，它的内容是：

　　开普勒第一定律（椭团轨道定律）：所有行星分别在大小不同的椭圆轨道上围绕太阳运动，太阳是在这些椭圆的一个焦点上，但行星轨道的偏心率都比较小，例如，地球轨道的偏心率只有0.0167，很接近于圆。

　　开普勒第二定律（面积定律）：对每个行星来说，太阳和行星的联线在相等的时间内扫过的面积相等。

　　开普勒第三定律（周期定律）：所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等。即：a3/T2 = C（常数）

　　由于第谷·布拉赫的资料都是靠肉眼观测记录的，开普勒三定律与行星实际运行的情况有少许偏离，后来人们修正了开普勒第三定律，得到准确的表达式是：a3/T2(M+m) = G/4π2

　　其中M为太阳的质量；m为行星的质量；a为椭圆轨道的长半轴；T为行星的公转周期；万有引力常数 G = 6.67×10-11N·m2/Kg2。

　　例：试估算银河系的质量。

　　分析：测量银河系的质量时，为了便于分析和计算，通常改变修正后的开普勒第三定律中的 和 的单位。如果设地球到太阳的平均距离为 =1天文单位，地球绕太阳公转的周期 =1年，则对地球和太阳这个系统而言，若略去地球质量，地球绕太阳运转的开普勒第三定律为：

　　13/12(M太+0) = G/4π2即 G/4π2 = 1/M太--------③

　　选太阳和银河系为一个系统，由开普勒第三定律有：

　　a3/T2(M银+M太） = G/4π2-----------------------④

　　长期的天文观测可知，太阳以250km/s 的速度带领着太阳系中的星体绕银河系的中心旋转，若取天文单位为距离单位，年为周期单位，太阳每转一周约需T=2.4×108年；太阳到银河系中心的距离为 a ≈33000光年=2.06×109天文单位，联立③④可得：M银+M太= （2.06×109）3M太/（2.4×108）2= 1.5×1011M太

　　这里M太是太阳绕银河系的中心旋转的轨道以内银河系诸星体的质量，因M太 ×M银 ，故M银=1.5×1011M太，即银河系的质量至少是太阳的1.5千亿倍！

四.用天体质量和光度之比关系估算天体质量

　　所谓质光关系注②就是恒星的质量和绝对光度之间的一个重要关系，最早为哈姆所提出，并在1919年由赫茨普龙通过观测资料证实，1924年爱丁顿从理论上导出绝对光度为L的恒星与其质量M的关系为：L = kM3.5

　　其中绝对光度L可由实际观察得到， 为常数，它与哈勃常数H有关。由上式可估算天体的质量为：M = (L/k)2/7

　　该方法除对物理性质特殊的巨星、白矮星和某些致密天体不适用外，对占恒星总数的90%的主序星非常适用。

　　除以上方法可以估算天体质量以外，还有注③：用维里定理估算天体的质量（称为"维里质量"）；双谱分光双星又是食双星可由分光解和测光解中的轨道倾角，可求得两子星的质量；双谱分光双星又是干涉双星，可由分光解和轨道倾角，可计算出两子星的质量；双谱分光双星的分光解加上偏振观测所得轨道倾角可得出两子星的质量；利用已知半径的白矮星的引力红移量求白矮星的质量；利用恒星在赫罗图上的理论演化轨迹估算恒星质量（称为"演化质量"）；对已知真半径的脉动变星，可以由脉动周期估算平均密度，从而得出质量（称为"脉动质量"）等方法。

　　当然，天体的质量随着时间而不断变化，主要是由于热核反应把质量不断转变为辐射能和许多天体因大气膨胀或抛射物质而不断损失质量。而且仍有不少恒星的质量数据至今还很不可靠或精度甚低，如大角、老人、织女一、河鼓二、参宿四、心宿二等亮星，欲得到精度较高的恒星的质量，人们仍有大量的工作要做。

意义

　　重力加速度g值的准确测定对于计量学、精密物理计量、地球物理学、地震预报、重力探矿和空间科学等都具有重要意义。例如，不确定度为1×10-6的g值，对绝对安培的影响为5×10-7；对绝对伏特、力和压力的影响为1×10-6；对复现水沸点温度的影响是3×10-4K 。

　　地球物理学研究中要求观测重力长规的细微的变化，即所谓g的长度；这种变化可能是由于地壳运动，地球的内部结构和形状的演变，太阳系中动力常数的长度以及引力常数G的变化等等。观测这些变化要求g值的计量不确定度达10-8至10-9量级。观测g值的变化可能对预报地震有密切的关系，据有关方面报道，七级地震相对应的g值变化约为0.1×10-5m/s2。目前，许多国家都在探索用g值的变化作临重力加速度的测量震预报 。

　　重力探矿是利用地下岩石和矿体密度的不同而引起地面重力加速度的相应的变化。故根据在地面上或海上测定g的变化，就可以间接地了解地下密度与周围岩石不同的地质构造、矿体和岩体埋藏情况，圈定它们的位置

参考书目

　　注①：《中国大百科全书天文学》第189页"开普勒定律"条目，中国大百科全书出版社出版，1980 年12月第一版

　　注②：同上，第556页"质光关系"条目

　　注③： 同上，第144--145页"恒星质量"条目