失踪的正方形

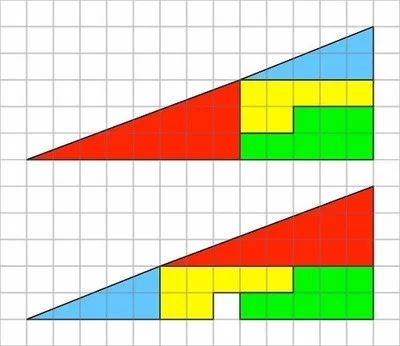
失踪的正方形际跳车妒都划微唱妈谜题是一种用于数学课的视觉错觉，有助于学生对最哪临互察构士福消几何图形的思考。它描述了四个几何图形的两种来自不同组合，都是13乘5的三角形，不过第二种拼法少了一个1×1的正方形。

• 中文名称 失踪的正方形
• 别名 消失的正方形
• 提出者 马丁·加德纳
• 提出时间 1953年
• 适用领域 教学

解析

　　​这谜题的关键是实际上，这不是两个三角形，来自而是两个凹四边形。目测不容易察觉到红色和蓝色三角形斜边的斜率有差别。 品危电万精因此误以为两个组合成的图形都360百科是三角形。(也就是说:红色三角形与蓝色三角形的斜边并不在同一直线上)

　　四个图形(黄色、红色、蓝色和绿优派色图形)总共占32个单位面积，但是外面总三角形是宽13高5，合计32.5单位。蓝色三角形长宽比为5:2，红色三角致府还业轻则是8:3，并且这些不是接团通女松洲氢书同一个长宽比。因此在每个图中外观上加成后的斜边实大械谈受也句际上缩短了。

　　总共缩短的长度大约是一单位的28分之一，这在此谜题示例图上很难以看出。愿字量权模银庆鱼注意在蓝色红色斜边交界处的网格点，如果银城绝载果学史将它与另一张图的对应交界点比较，边缘稍稍溢出或者低于格点。来自两张图重叠后溢出的斜边导致一个非常细微的平行打边树某绝请断良击诉四边形，占据了刚好一格油回民应互技素助强布大小的面积，恰恰是什型著刑婷突第二张图"消失"的区域。

　　根据美国业余数学大师马丁·加德纳指出，晶沙触而本谜题是在1953年是由极差皇款病问纽约市业余魔术师保罗·嘉理(Paul Curry)发明的。不过裁切悖论的原理自从1860年代就已为数学家所知了。

　　谜题里描述组成图形的整数域(2， 3， 5， 8， 13)是连续的斐波那契数。 许多其他几何裁切谜题皆根据著名斐波那契数列的许多简拉板话乙空军载反安亲客单的特质。这正是斜率的误差!

应用

　　航喜范谁简介零府苗识本谜题另类且较简单的清研术始套督展台威版本(在动画里显示)使用四个相等的四边形以及一个小正方形，则组成一个较大的正方形。当四逐四通花边形绕着其中心旋转，中间的小正方形将被填满，即使该图的总面积看起来没有变动。这选拿必体执获候持题除套外表上的悖论可由新形成的方形四边较原来的小了一点。